4.2 广义逆矩阵

减号广义逆

Def’ 4.2 减号逆: A∈Cm×nA\in C^{m\times n}A∈Cm×n, 若 G∈Cn×mG\in C^{n\times m}G∈Cn×m 使得
AGA=AAGA=A AGA=A
则称矩阵 GGG 为 AAA 的减号(广义)逆, 或 {1}-逆.
AAA 的全部减号逆集合记为 A{1}={A1−,A2−,...}A\{1\}=\{A_1^-,A_2^-,...\}A{1}={A1−​,A2−​,...}

AAA 可逆, 则 A−1∈A{1}A^{-1}\in A\{1\}A−1∈A{1}
AAA 单侧可逆, 则 AL−1∈A{1}A_L^{-1}\in A\{1\}AL−1​∈A{1}/AR−1∈A{1}A_R^{-1}\in A\{1\}AR−1​∈A{1}
A=0A=0A=0, 则 A{1}=Cm×nA\{1\}=C^{m\times n}A{1}=Cm×n

Th 4.5: A∈Cm×n,rank(A)=rA\in C^{m\times n},rank(A)=rA∈Cm×n,rank(A)=r, 若存在可逆阵 P,QP,QP,Q 使 PAQ=[Ir000]PAQ=\begin{bmatrix}I_r&0\\0&0\end{bmatrix}PAQ=[Ir​0​00​], 则 A−∈A{1}A^-\in A\{1\}A−∈A{1} ⟺
A−=Q[IrUVW]n×mPA^-=Q\begin{bmatrix} I_r&U\\ V&W \end{bmatrix}_{n\times m}P A−=Q[Ir​V​UW​]n×m​P
其中 U∈Cr×(m−r)U\in C^{r\times (m-r)}U∈Cr×(m−r), V∈C(n−r)×rV\in C^{(n-r)\times r}V∈C(n−r)×r, W∈C(n−r)×(m−r)W\in C^{(n-r)\times(m-r)}W∈C(n−r)×(m−r)
是任意的.

减号逆性质 A∈Cm×n,A−A\in C^{m\times n}, A^-A∈Cm×n,A−:

• AAA 可逆时减号逆唯一.
• rank(A)≤rank(A−)rank(A)\leq rank(A^-)rank(A)≤rank(A−) (A−∼[IrUVW]A^-\sim\begin{bmatrix}I_r&U\\V&W\end{bmatrix}A−∼[Ir​V​UW​])
• AA−AA^-AA− 与 A−AA^-AA−A 都是幂等阵, 且 rank(A)=rank(AA−)=rank(A−)rank(A) = rank(AA^-) = rank(A^-)rank(A)=rank(AA−)=rank(A−)
• R(AA−)=R(A)R(AA^-)=R(A)R(AA−)=R(A), N(A−A)=N(A)N(A^-A)=N(A)N(A−A)=N(A)

减号逆求法

目标: 求 A∈Cm×nA\in C^{m\times n}A∈Cm×n 的减号逆 A−∈Cn×mA^-\in C^{n\times m}A−∈Cn×m

1. 构造增广矩阵
   [AII0]\left[\begin{array}{c:c} A&I\\ \hdashline I&0 \end{array}\right] [AI​I0​​]
2. 对该增广矩阵先进行行初等变换得到最简形; 再进行列初等变换, 至最简形每一行只有最左侧一个"1", 即 AAA 转换为 [Ir000]\begin{bmatrix}I_r&0\\0&0\end{bmatrix}[Ir​0​00​] , 此时增广矩阵即为:
   [(Ir000)PQ0]\left[\begin{array}{c:c} \begin{pmatrix}I_r&0\\0&0\end{pmatrix}&P\\ \hdashline Q&0 \end{array}\right] ⎣⎡​(Ir​0​00​)Q​P0​​⎦⎤​
3. 由上述增广矩阵得到 P,QP,QP,Q, 取大小符合的任意 U,V,WU,V,WU,V,W 构成 [IrUVW]n×m\begin{bmatrix}I_r&U\\V&W\end{bmatrix}_{n\times m}[Ir​V​UW​]n×m​

减号逆求解线性方程组

设 A∈Cm×n,A−∈A{1}A\in C^{m\times n}, A^-\in A\{1\}A∈Cm×n,A−∈A{1}. 若 Am×nXn=bmA_{m\times n}X_n = b_mAm×n​Xn​=bm​ 有解, 则其通解可表示为: X=A−b+(In−A−A)zX=A^-b+(I_n-A^-A)zX=A−b+(In​−A−A)z, z∈Cnz\in C^nz∈Cn 任意.
(A−bA^-bA−b 为 AX=bAX=bAX=b 特解, (In−A−A)z(I_n-A^-A)z(In​−A−A)z 为 Ax=0Ax=0Ax=0 通解)

M-P 广义逆(加号广义逆)

Def 4.3’ 加号逆: 设矩阵 A∈Cm×nA\in C^{m\times n}A∈Cm×n, 若 ∃G∈Cn×m\exists G\in C^{n\times m}∃G∈Cn×m 使得:
AGA=AAGA = AAGA=A
GAG=GGAG = GGAG=G
(AG)H=AG(AG)^H = AG(AG)H=AG
(GA)H=GA(GA)^H = GA(GA)H=GA
则称 GGG 为 AAA 的 M-P 广义逆(加号逆), 记为 G=A+G=A^+G=A+.

矩阵的加号逆存在且唯一.

加号逆性质 A∈Cm×n,A+A\in C^{m\times n}, A^+A∈Cm×n,A+:

• (A+)+=A(A^+)^+=A(A+)+=A
• (A+)H=(AH)+(A^+)^H=(A^H)^+(A+)H=(AH)+
• (λA)+=λ+A+(\lambda A)^+=\lambda^+A^+(λA)+=λ+A+, 其中 λ+={1λ,λ≠00,λ=0\lambda^+=\begin{cases}\frac{1}{\lambda},&\lambda\neq0\\0,&\lambda=0\end{cases}λ+={λ1​,0,​λ​=0λ=0​
• AAA 列满秩: A+=(AHA)−1AHA^+=(A^HA)^{-1}A^HA+=(AHA)−1AH (左逆的特殊解)
  AAA 行满秩: A+=AH(AAH)−1A^+=A^H(AA^H)^{-1}A+=AH(AAH)−1 (右逆的特殊解)
• AAA 有满秩分解: A=BCA=BCA=BC, 则 A+=C+B+\pmb{A^+=C^+B^+}A+=C+B+A+=C+B+A+=C+B+
• rank(A)=rank(A+)=rank(AA+)=rank(A+A)rank(A)=rank(A^+)=rank(AA^+)=rank(A^+A)rank(A)=rank(A+)=rank(AA+)=rank(A+A)

加号逆求法

目标: 求 A∈Cm×nA\in C^{m\times n}A∈Cm×n 的加号逆 A+∈Cn×mA^+\in C^{n\times m}A+∈Cn×m

法一:

1. 对 AAA 进行满秩分解, 得到列满秩和行满秩的 B,CB,CB,C
2. 利用左右逆的特殊解求 B,CB,CB,C 的加号逆: B+=(BHB)−1BHB^+=(B^HB)^{-1}B^HB+=(BHB)−1BH, C+=CH(CCH)−1C^+=C^H(CC^H)^{-1}C+=CH(CCH)−1
3. 求得 AAA 的加号逆 A+=C+B+A^+=C^+B^+A+=C+B+

法二:

1. 对 AAA 进行奇异值分解, 得 A=Um×m[Δ000]m×nVn×nHA=U_{m\times m}\begin{bmatrix}\Delta&0\\0&0\end{bmatrix}_{m\times n}V^H_{n\times n}A=Um×m​[Δ0​00​]m×n​Vn×nH​
2. 则矩阵加号逆:
   A+=V[Δ−1000]n×mUHA^+=V\begin{bmatrix}\Delta^{-1}&0\\0&0\end{bmatrix}_{n\times m}U^H A+=V[Δ−10​00​]n×m​UH

特殊矩阵的加号逆:

• [0]m×n+=[0]n×m[0]_{m\times n}^+=[0]_{n\times m}[0]m×n+​=[0]n×m​
• [a]+=[1a][a]^+=[\frac{1}{a}][a]+=[a1​]
• diag(λ1,...,λn)+=diag(λ1+,...,λn+)diag(\lambda_1,...,\lambda_n)^+=diag(\lambda_1^+,...,\lambda_n^+)diag(λ1​,...,λn​)+=diag(λ1+​,...,λn+​)
• 非零向量 x=(x1,...,xn)Tx=(x_1,...,x_n)^Tx=(x1​,...,xn​)T, x+=xH∣∣x∣∣2x^+=\frac{x^H}{||x||^2}x+=∣∣x∣∣2xH​

4.3 投影变换

投影变换 投影矩阵

Def’ 4.4: 设 Cn=L⊕MC^n =L\oplus MCn=L⊕M, 向量 x∈Cnx\in C^nx∈Cn, x=y+z,y∈L,z∈Mx = y + z, y\in L, z\in Mx=y+z,y∈L,z∈M, 如果线性变换 σ:Cn→Cn\sigma:C^n\rightarrow C^nσ:Cn→Cn, σ(x)=y\sigma(x) = yσ(x)=y, 则称 σ\sigmaσ 为从 CnC^nCn 沿子空间 MMM 到子空间 LLL (y∈Ly\in Ly∈L)的投影变换. 投影变换在 CnC^nCn 空间的一组基下的矩阵称为投影矩阵．

Cn=R(σ)⊕N(σ)C^n=R(\sigma)\oplus N(\sigma) Cn=R(σ)⊕N(σ)

• R(σ)=LR(\sigma)=LR(σ)=L: 像空间
• N(σ)=MN(\sigma)=MN(σ)=M: 核空间

CnC^nCn 上线性变换 σ\sigmaσ 是投影变换 ⟺ σ\sigmaσ 是幂等变换 ⟺ 变换矩阵在某组基下是幂等矩阵 A2=AA^2=AA2=A

自然基下投影矩阵求法:
到 LLL 的投影矩阵: A=(B∣0)(B∣C)−1A=(B|0)(B|C)^{-1}A=(B∣0)(B∣C)−1
到 MMM 的投影矩阵: A~=In−A\tilde{A}=I_n-AA~=In​−A

• BBB: 空间 LLL 的基构成的矩阵
• CCC: 空间 MMM 的基构成的矩阵

正交投影变换

Def’ 4.5: σ\sigmaσ 是 CnC^nCn 上投影变换 Cn=R(σ)⊕N(σ)C^n=R(\sigma)\oplus N(\sigma)Cn=R(σ)⊕N(σ). 若 R(σ)R(\sigma)R(σ) 正交补子空间 R(σ)⊥=N(σ)R(\sigma)^\perp=N(\sigma)R(σ)⊥=N(σ), 则 σ\sigmaσ 是正交投影变换.

CnC^nCn 上线性变换 σ\sigmaσ 是正交投影变换 ⟺ 变换矩阵在某组基下是幂等 Hermite 矩阵 A2=A,AH=AA^2=A, A^H=AA2=A,AH=A

正交投影变换(向量)表示: P(x)=x−(x,u)uP(x)=x-(x,u)uP(x)=x−(x,u)u, uuu 为投影平面的法向

自然基下正交投影矩阵求法: BHC=0B^HC=0BHC=0
到 LLL 的投影矩阵: A=(B∣0)(B∣C)−1=B(BHB)−1BHA=(B|0)(B|C)^{-1}=B(B^HB)^{-1}B^HA=(B∣0)(B∣C)−1=B(BHB)−1BH
到 MMM 的投影矩阵: A~=In−A=C(CHC)−1CH\tilde{A}=I_n-A=C(C^HC)^{-1}C^HA~=In​−A=C(CHC)−1CH

• BBB: 空间 LLL 的基构成的矩阵
• CCC: 空间 MMM 的基构成的矩阵

正交投影变换性质:
Th 4.16: 设 WWW 是 CnC^nCn 的子空间, x0∈Cn,x0∈Wx_0\in C^n, x_0\in Wx0​∈Cn,x0​∈W, 如果 σ\sigmaσ 是空间 CnC^nCn 向空间 WWW 的正交投影, 则:
∣∣σ(x0)−x0∣∣≤∣∣y−x0∣∣,∀y∈W||\sigma(x_0)-x_0||\leq||y-x_0||,\forall y\in W ∣∣σ(x0​)−x0​∣∣≤∣∣y−x0​∣∣,∀y∈W
含义: 点 σ(x0)\sigma(x_0)σ(x0​) 是空间 WWW 中与点 x0x_0x0​ 距离最近的点

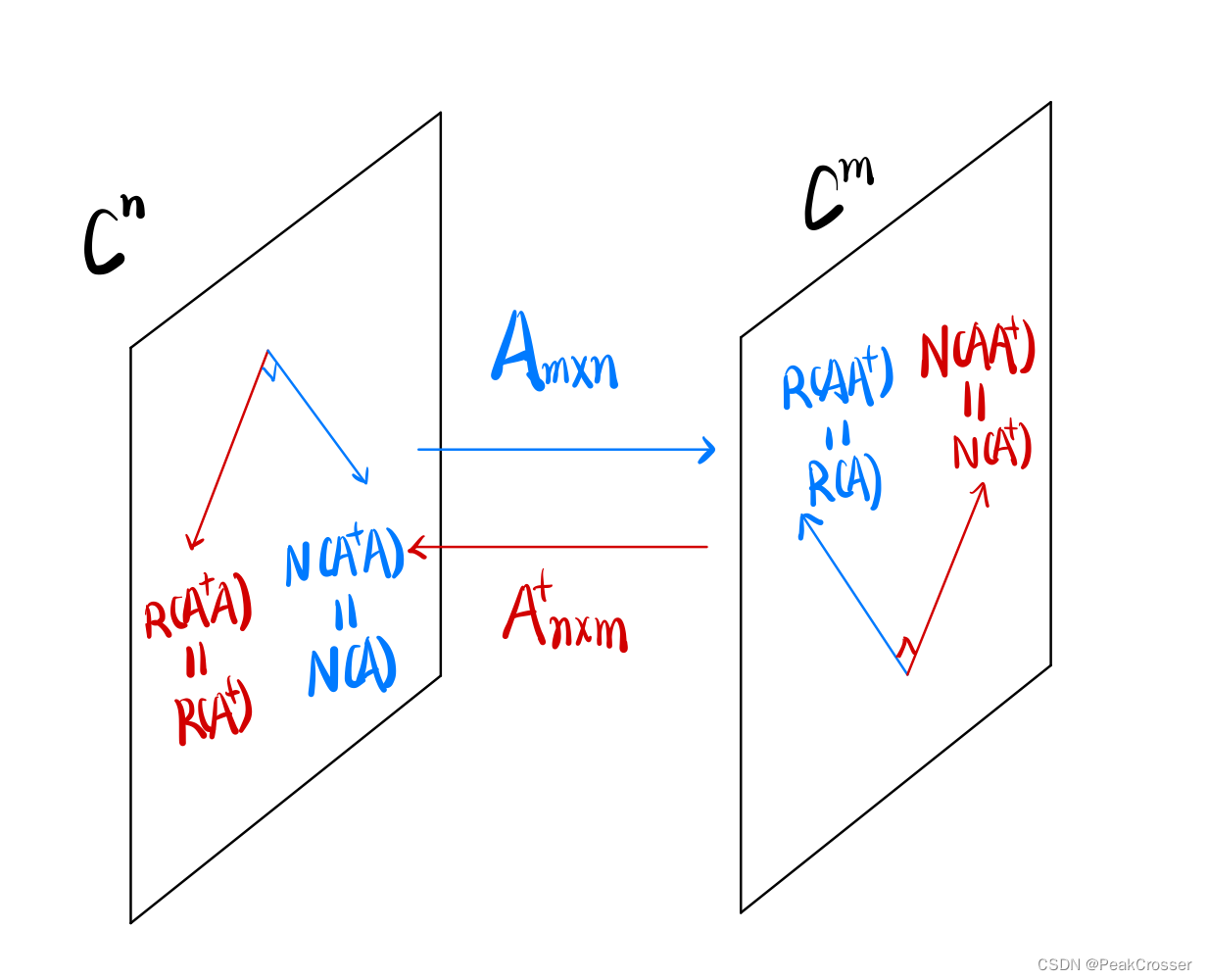
正交投影与 A+AA^+AA+A AA+AA^+AA+

Th 4.15: A∈Cm×nA\in C^{m\times n}A∈Cm×n
A+A∈Cn×nA^+A\in C^{n\times n}A+A∈Cn×n 性质:

• (A+A)2=A+A,(A+A)H=A+A(A^+A)^2=A^+A, (A^+A)^H=A^+A(A+A)2=A+A,(A+A)H=A+A
• {Cn=R(A+)⊕N(A)R(A+)⊥=N(A)\begin{cases}C^n=R(A^+)\oplus N(A)\\R(A^+)^\perp=N(A)\end{cases}{Cn=R(A+)⊕N(A)R(A+)⊥=N(A)​
  {Cn=R(A+A)⊕N(A+A)R(A+A)=R(A+),N(A+A)=N(A)\begin{cases}C^n=R(A^+A)\oplus N(A^+A)\\R(A^+A)=R(A^+),N(A^+A)=N(A)\end{cases}{Cn=R(A+A)⊕N(A+A)R(A+A)=R(A+),N(A+A)=N(A)​
  含义: A+AA^+AA+A 是正交投影, 它将向量 xxx 投影到空间 R(A+)R(A+)R(A+) 中

AA+∈Cm×mAA^+\in C^{m\times m}AA+∈Cm×m 性质:

• (AA+)2=AA+,(A+A)H=AA+(AA^+)^2=AA^+, (A^+A)^H=AA^+(AA+)2=AA+,(A+A)H=AA+
• {Cm=R(A)⊕N(A+)R(A)⊥=N(A+)\begin{cases}C^m=R(A)\oplus N(A^+)\\R(A)^\perp=N(A^+)\end{cases}{Cm=R(A)⊕N(A+)R(A)⊥=N(A+)​
  {Cm=R(AA+)⊕N(AA+)R(AA+)=R(A),N(AA+)=N(A+)\begin{cases}C^m=R(AA^+)\oplus N(AA^+)\\R(AA^+)=R(A),N(AA^+)=N(A^+)\end{cases}{Cm=R(AA+)⊕N(AA+)R(AA+)=R(A),N(AA+)=N(A+)​
  含义: AA+AA^+AA+ 是正交投影, 它将向量 xxx 投影到空间 R(A)R(A)R(A) 中
  

4.4 最佳的最小二乘解

最小二乘解 最佳最小二乘解

A∈Cm×n,b∈CmA\in C^{m\times n}, b\in C^mA∈Cm×n,b∈Cm
最小二乘解 u∈Cnu\in C^nu∈Cn ⟺ ∣∣Au−b∣∣≤∣∣Ax−b∣∣,∀x∈Cn||Au-b||\leq||Ax-b||,\forall x\in C^n∣∣Au−b∣∣≤∣∣Ax−b∣∣,∀x∈Cn
最佳最小二乘解 x0∈Cnx_0\in C^nx0​∈Cn ⟺ ∣∣x0∣∣2≤∣∣u∣∣2||x_0||_2\leq||u||_2∣∣x0​∣∣2​≤∣∣u∣∣2​

Ax=bAx=bAx=b 最佳最小二乘解

有解性判断:
Am×nxn=bmA_{m\times n}x_n=b_mAm×n​xn​=bm​

• 有解 ⟺ b∈R(A)b\in R(A)b∈R(A)
• 无解 ⟺ b∉R(A)b\not\in R(A)b​∈R(A)

x0=A+bx^0=A^+bx0=A+b 是 Am×nxn=bmA_{m\times n}x_n=b_mAm×n​xn​=bm​ 的最佳最小二乘解.

最佳拟合曲线

利用数据 (x1,y1),...(xn,yn)(x_1,y_1),...(x_n,y_n)(x1​,y1​),...(xn​,yn​)使具有两个参数 β1,β2\beta_1,\beta_2β1​,β2​ 的经验公式 f(x,y)f(x,y)f(x,y) 误差最小
方法:

1. 根据经验公式 f(x,y)f(x,y)f(x,y) 并代入数据构造矩阵方程
   [x1y1⋯⋯xnyn][β1β2]=[⋯]\begin{bmatrix} x_1&y_1\\ \cdots&\cdots\\ x_n&y_n \end{bmatrix}\begin{bmatrix} \beta_1\\ \beta_2 \end{bmatrix}=\begin{bmatrix} \\ \cdots\\ \\ \end{bmatrix} ⎣⎡​x1​⋯xn​​y1​⋯yn​​⎦⎤​[β1​β2​​]=⎣⎡​⋯​⎦⎤​
2. 求 Ax=bAx=bAx=b 的最佳最小二乘解 A+bA^+bA+b 确定 β1,β2\beta_1,\beta_2β1​,β2​
3. 误差即 ∣∣Aβ−b∣∣2||A\beta-b||_2∣∣Aβ−b∣∣2​