🔥 本文由 程序喵正在路上 原创，CSDN首发！
💖 系列专栏：数据结构与算法
🌠 首发时间：2022年12月5日
🦋 欢迎关注🖱点赞👍收藏🌟留言🐾
🌟 一以贯之的努力 不得懈怠的人生

阅读指南

• 查找
• • 基本概念
  • 对查找表的常见操作
  • 查找算法的评价指标
• 顺序查找
• • 算法思想
  • 实现
  • 顺序查找的优化（对有序表）
  • 用查找判定树分析ASL
  • 顺序查找的优化（被查概率不相等）
• 折半查找
• • 算法思想
  • 实现
  • 查找效率分析
  • 折半查找判定树的构造
  • 查找效率
• 分块查找
• • 算法思想
  • 查找效率分析

查找

基本概念

查找 —— 在数据集合中寻找满足某种条件的数据元素的过程称为查找

查找表（查找结构） —— 用于查找的数据集合称为查找表，它由同一类型的数据元素（或记录）组成

关键字 —— 数据元素中唯一识别该元素的某个数据项的值，使用基于关键字的查找，查找结果应该是唯一的

对查找表的常见操作

1. 查找符合条件的数据元素
2. 插入、删除某个数据元素

只需进行操作 111 的为静态查找表，我们只关注查找速度即可；

两种操作都要进行的为动态查找表，除了查找速度，我们也要关注插入或删除操作是否方便实现

查找算法的评价指标

查找长度 —— 在查找运算中，需要对比关键字的次数称为查找长度

平均查找长度（ASL,AverageSearchLengthASL, Average \ Search \ LengthASL,Average Search Length）—— 所有查找过程中进行关键字的比较次数的平均值

平均查找长度计算方式如下：
ASL=∑i=1nPiCiASL = \sum_{i=1}^{n}P_iC_i ASL=i=1∑n​Pi​Ci​
其中，nnn 为数据元素的个数，PiP_iPi​ 为查找第 iii 个元素的概率，CiC_iCi​ 为查找第 iii 个元素的查找长度。通常情况下，默认查找任何一个元素的概率是相同的

ASLASLASL 的数量级反映了查找算法的时间复杂度，评价一个查找算法的效率时，通常需要考虑查找成功和查找失败两种情况的 ASLASLASL

顺序查找

算法思想

顺序查找，又称为线性查找，通常用于线性表，线性表又分为顺序表和链表两种

算法思想：从头到尾一个个找，或者反过来也行

实现

第一种方法（常规）：

typedef struct{				//查找表的数据结构（顺序表）ElemType *elem;			//动态数组基址int TableLen;			//表的长度
}SSTable;//顺序查找
int Search_Seq(SSTable ST, ElemType key) {int i;//当找到或者找完就会跳出循环for (i = 0; i < ST.TableLen && ST.elem[i] != key; ++i);//查找成功则返回元素下标；否则返回-1return i == ST.TableLen ? - 1 : i;	
}

第二种方法（哨兵）：

此时数据从下标为 111 处开始存储，000 处作为哨兵

typedef struct{				//查找表的数据结构（顺序表）ElemType *elem;			//动态数组基址int TableLen;			//表的长度
}SSTable;//顺序查找
int Search_Seq(SSTable ST, ElemType key) {ST.elem[0] = key;		//将要查找的值存进 0 处int i;//从后遍历for (i = ST.TableLen; ST.elem[i] != key; --i);//查找成功则返回元素下标；否则返回0return i;	
}

优点：无需判断是否越界，效率更高

查找成功的 ASLASLASL：1+2+3+⋯+nn=n+12\frac{1 + 2+3 + \cdots + n}{n} = \frac{n+1}{2}n1+2+3+⋯+n​=2n+1​

查找失败的 ASLASLASL：n+1n + 1n+1

顺序查找的优化（对有序表）

查找表中元素有序存放（递增 / 递减），例如 713192937437 \ 13 \ 19 \ 29 \ 37 \ 437 13 19 29 37 43，当我们要找 212121 这个值时，一共有 n+1n+1n+1 种查找失败的情况，此时查找失败的 ASLASLASL 为 1+2+3+⋯+n+nn+1=n2+nn+1\frac{1 + 2+3 + \cdots + n + n}{n+1} = \frac{n}{2} + \frac{n}{n+1}n+11+2+3+⋯+n+n​=2n​+n+1n​

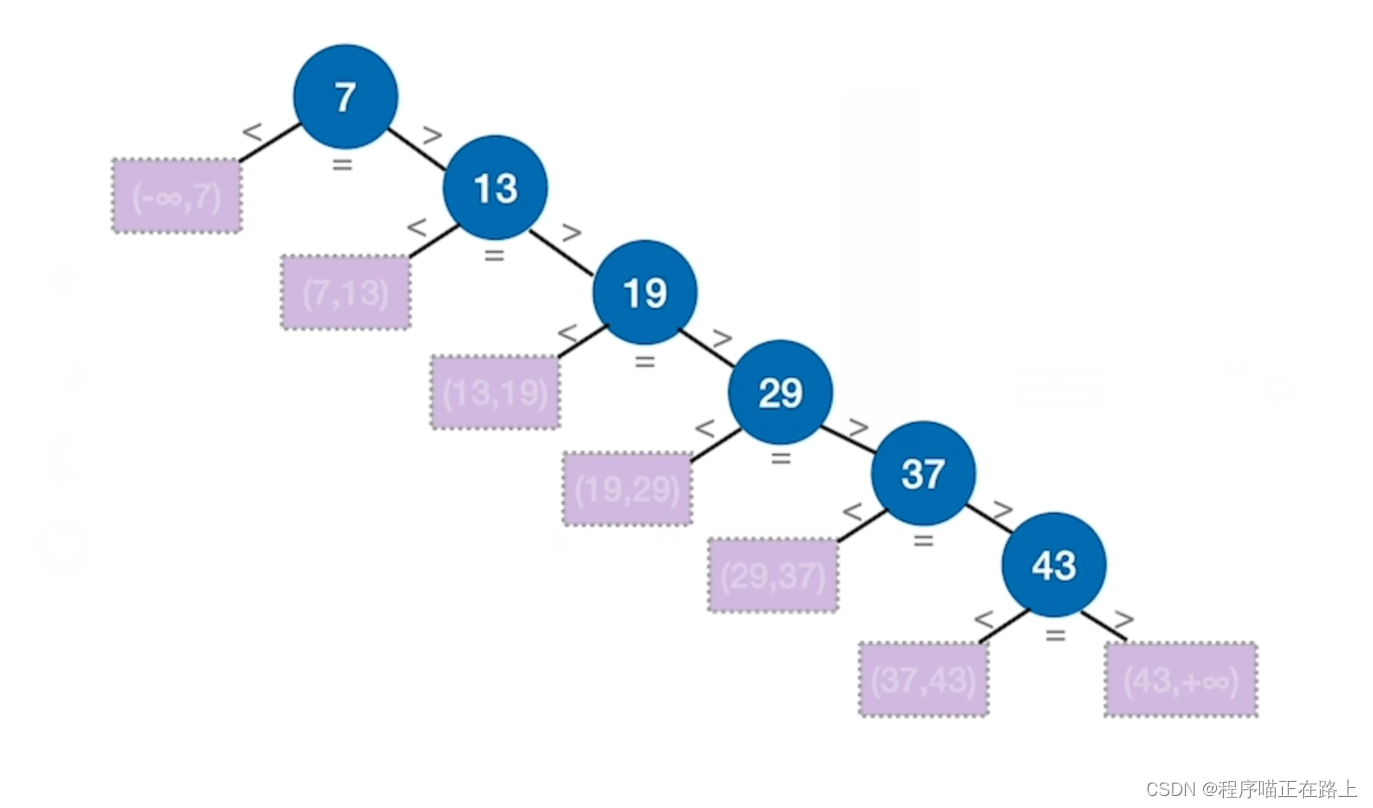
用查找判定树分析ASL

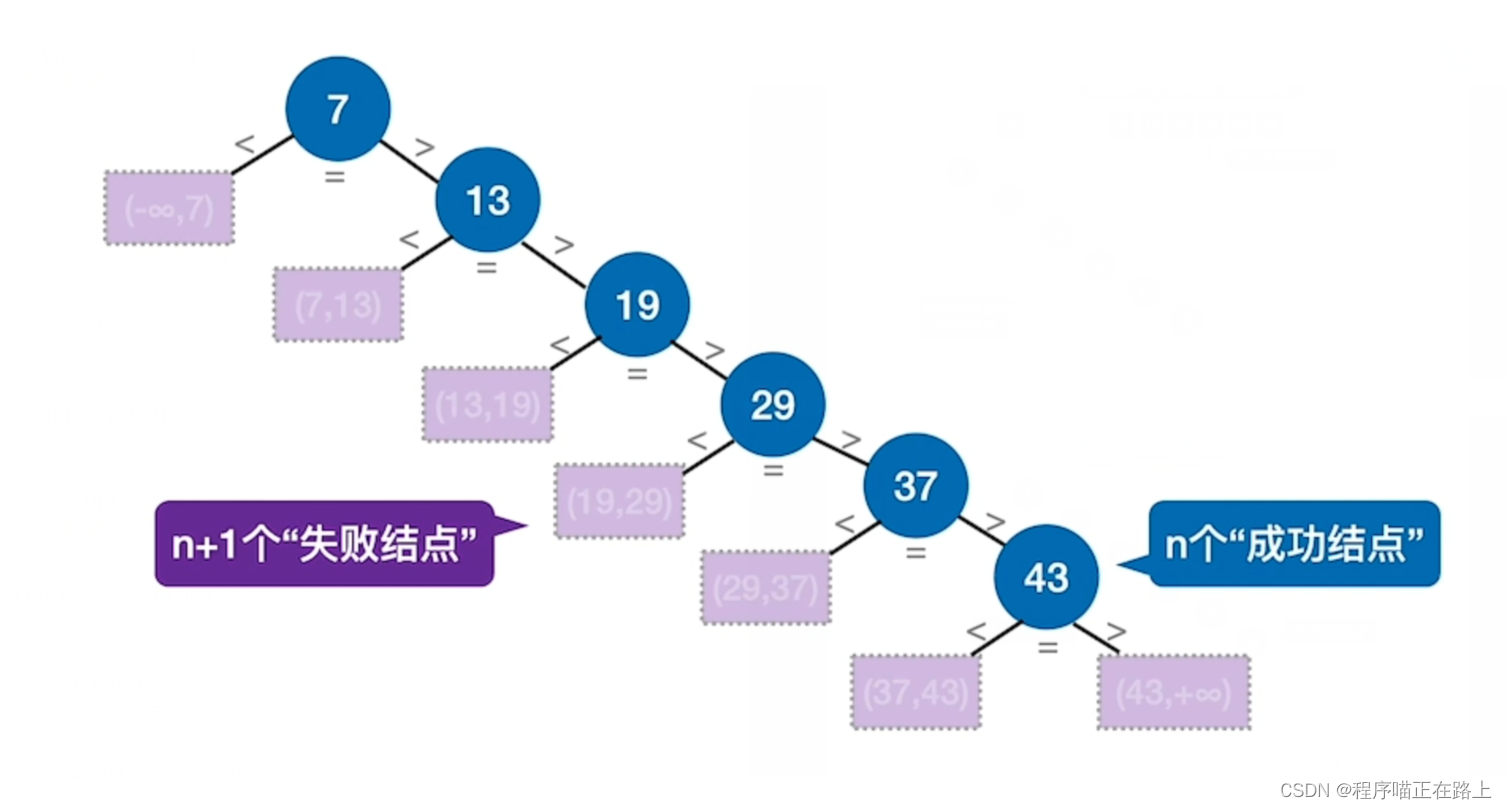
一个成功结点的查找长度 = 自身所在层数

一个失败结点的查找长度 = 其父节点所在层数

默认情况下，各种失败情况或成功情况都等概率发生

顺序查找的优化（被查概率不相等）

如果每个元素的被查概率不相等，我们可以将被查概率大的放在靠前位置，这样可以减小查找成功的 ASLASLASL

折半查找

算法思想

折半查找，又称为 “二分查找”，仅适用于有序的顺序表

实现

以下代码基于数据是存储在升序的顺序表

typedef struct{				//查找表的数据结构（顺序表）ElemType *elem;			//动态数组基址int TableLen;			//表的长度
}SSTable;//折半查找
int Binary_Search(SSTable L, ElemType key) {int low = 0, high = L.TableLen - 1, mid;while (low <= high) {mid = (low + high) / 2;		//取中间位置if (L.elem[mid] == key) return mid;				//查找成功返回所在位置else if (L.elem[mid] > key)high = mid - 1;			//中间值比查找值要大else low = mid + 1;			//中间值比查找值要小}return -1;		//查找失败
}

查找效率分析

假设有如下顺序表：

经过折半查找，我们可以得到一个它的查找判定树：

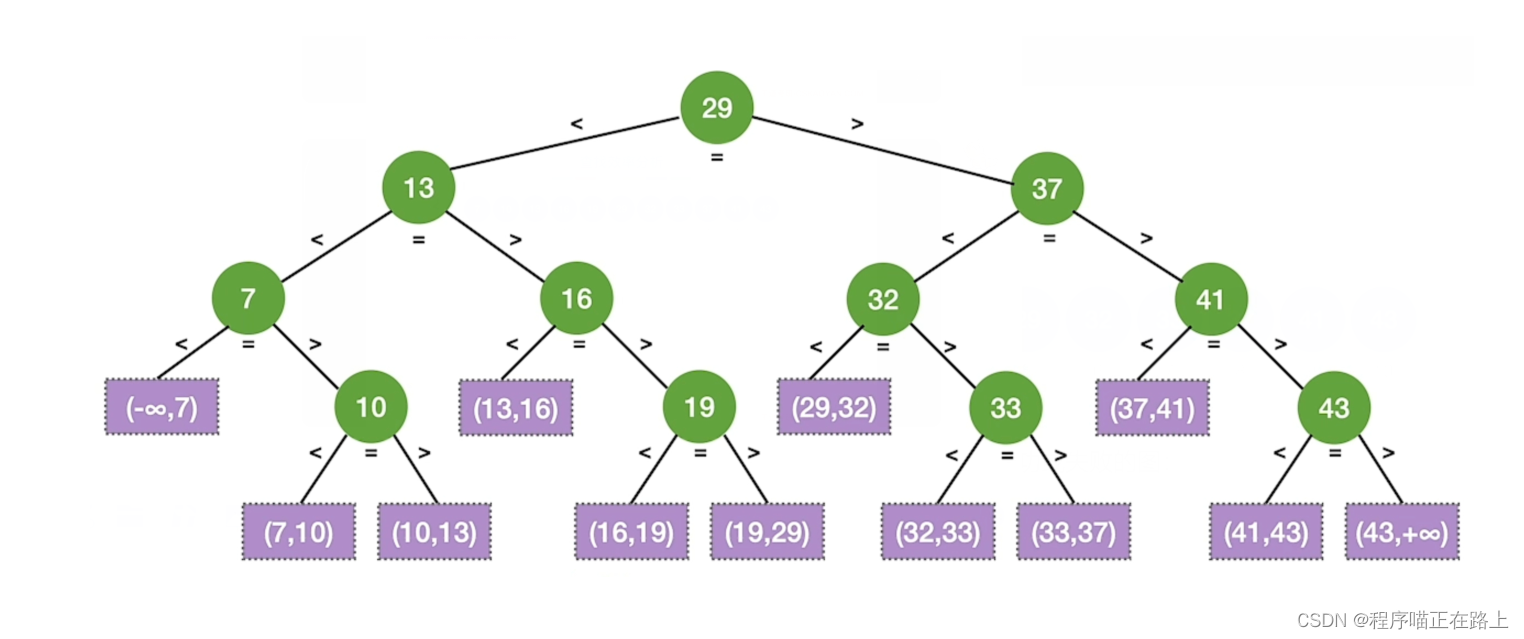
注：绿色部分为查找成功，紫色部分为查找失败

成功的平均查找长度为：(1×1+2×2+3×4+4×4)/11=3(1 \times 1 + 2 \times 2 + 3 \times 4 + 4 \times 4) / 11 = 3(1×1+2×2+3×4+4×4)/11=3

失败的平均查找长度为：(3×4+4×8)/12=11/3(3 \times 4 + 4 \times 8) / 12 = 11/3(3×4+4×8)/12=11/3

折半查找判定树的构造

• 如果当前 lowlowlow 和 highhighhigh 之间有奇数个元素，则 midmidmid 分隔后，左右两部分元素个数相等

• 如果当前 lowlowlow 和 highhighhigh 之间有偶数个元素，则 midmidmid 分隔后，左半部分比右半部分少一个元素

基于以上两个结论，我们可以得到下面的推论：

• 折半查找的判定树中，若 mid=⌊(low+high)/2⌋mid = \lfloor(low + high)/2 \rfloormid=⌊(low+high)/2⌋，则对于任何一个结点，必有 —— 右子树结点数 −-− 左子树结点数 =0= 0=0 或 111

所以我们可以得到 1∼161 \sim 161∼16 个元素的折半查找判定树如下：

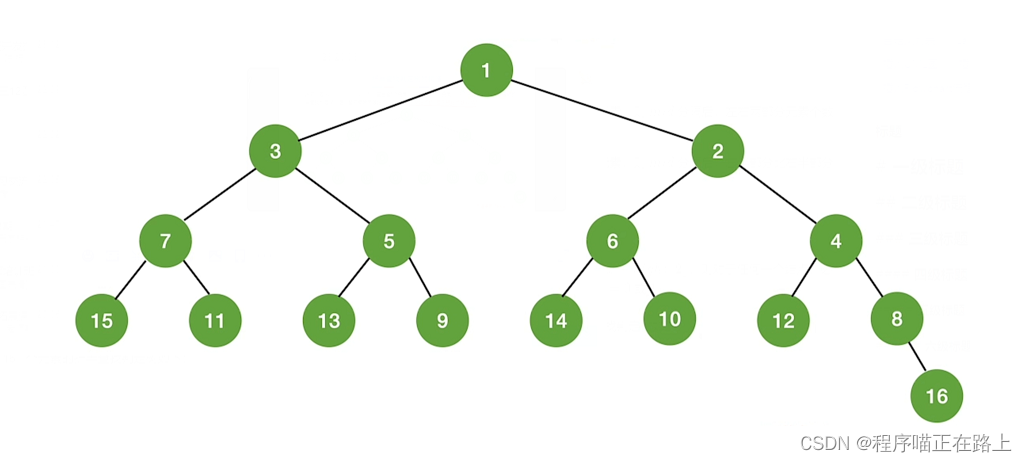
（注：图中的数字只是一个编号，不是值）

折半查找的判定树一定是平衡二叉树

折半查找判定树中，只有最下面一层是不满的，因此，元素个数为 nnn 时树高 h=⌈log2(n+1)⌉h = \lceil log_2(n + 1)\rceilh=⌈log2​(n+1)⌉（注：计算方法同 “完全二叉树”）

判定树结点关键字：左 < 中 < 右，满足二叉排序树的定义

若成功结点为 nnn 个，则失败结点为 n+1n + 1n+1 个（等于成功结点的空链域数量）

查找效率

树高 h=⌈log2(n+1)⌉h = \lceil log_2(n + 1)\rceilh=⌈log2​(n+1)⌉

查找成功的 ASL≤hASL \leq hASL≤h，查找失败的 ASL≤hASL \leq hASL≤h

所以折半查找的时间复杂度为 O(log2n)O(log_2n)O(log2​n)

分块查找

算法思想

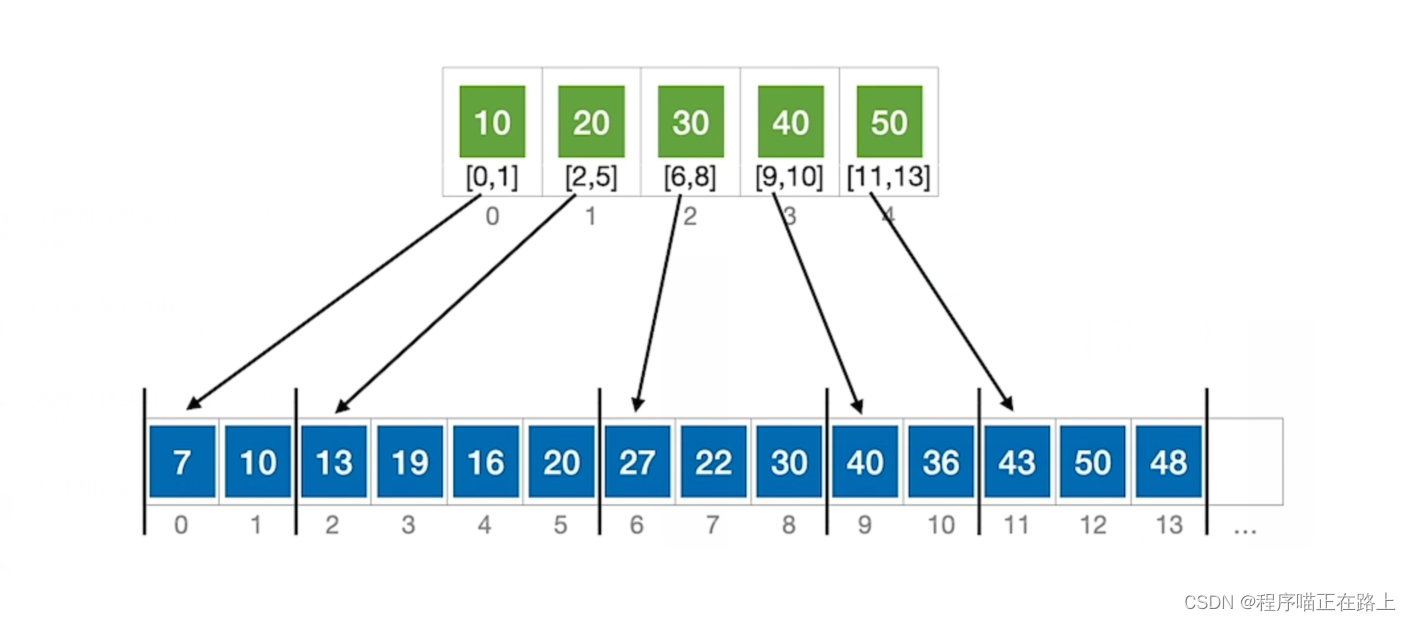
如上图，下面是顺序表，上面是对应的索引表，索引表中保存了每个分块的最大关键字和分块的存储区间

特点：块内无序，块间有序

//索引表
typedef struct{ElemType maxValue;int low, high;
}Index;//顺序表存储实际元素
ElemType List[100];

分块查找，又称为索引顺序查找，算法过程如下：

1. 在索引表中确定待查记录所属的分块（可顺序、可折半）
2. 在块内顺序查找

在进行折半查找所属分块时，如果索引表中不包含目标关键字，则折半查找索引表最终停在 low>highlow > highlow>high，这时候我们要在 lowlowlow 所指分块中查找

• 原因：最终 lowlowlow 左边一定小于目标关键字，highhighhigh 右边一定大于目标关键字，而分块存储的索引表中保存的是各个分块的最大关键字

查找效率分析

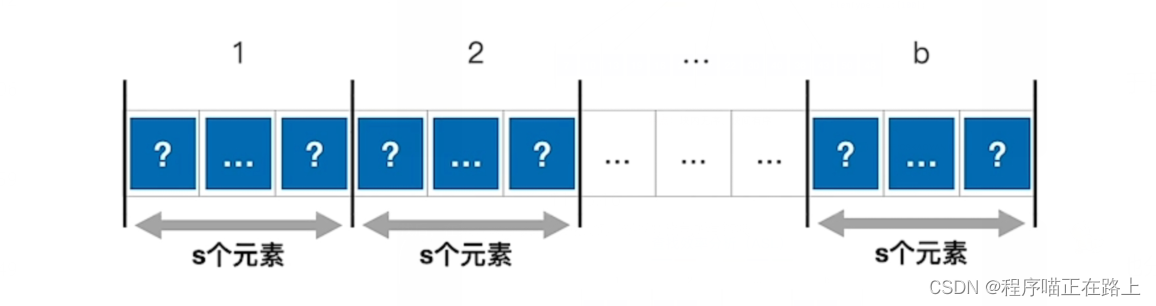
假设，长度为 nnn 的查找表被均匀地分为 bbb 块，每块 sss 个方块

设索引查找和块内查找的平均查找长度分别为 lIl_IlI​、LsL_sLs​，则分块查找的平均查找长度为
ASL=lI+LsASL = l_I + L_s ASL=lI​+Ls​
用顺序表查找索引表，则 LI=(1+2+⋯+b)b=b+12L_I = \frac{(1 + 2 + \dots + b)}{b} = \frac{b + 1}{2}LI​=b(1+2+⋯+b)​=2b+1​，Ls=(1+2+⋯+s)s=s+12L_s = \frac{(1 + 2 + \dots + s)}{s} = \frac{s + 1}{2}Ls​=s(1+2+⋯+s)​=2s+1​，那么 ASL=b+12+s+12=s2+2s+n2sASL = \frac{b + 1}{2} + \frac{s + 1}{2} = \frac{s^2 + 2s + n}{2s}ASL=2b+1​+2s+1​=2ss2+2s+n​，当 s=ns = \sqrt{n}s=n​ 时，ASLASLASL 最小，为 n+1\sqrt{n} + 1n​+1

用折半查找查索引表，则 LI=⌈log2(b+1)⌉,Ls=(1+2+⋯+s)s=s+12L_I = \lceil log_2(b + 1) \rceil, L_s = \frac{(1 + 2 + \cdots + s)}{s} = \frac{s + 1}{2}LI​=⌈log2​(b+1)⌉,Ls​=s(1+2+⋯+s)​=2s+1​， 则 ASL=⌈log2(b+1)⌉+s+12ASL = \lceil log_2(b + 1) \rceil + \frac{s + 1}{2}ASL=⌈log2​(b+1)⌉+2s+1​