确定性推理（Deterministic Reasoning）目录

• 一、推理基本概念
• 二、推理逻辑基础
• • 1. 命题逻辑（Propositional Logic）
  • 2. 谓词逻辑（Predicate Logic）
  • 3. 推理的控制策略
  • • (i) 推理方向
    • • (a) 正向推理：已知事实（条件）→结论
      • (b) 逆向推理：某个假象目标（结论）→已知条件
      • \(c\) 混合推理：把正向推理和逆向推理结合起来的推理
      • (d) 双向推理：正向与逆向推理同时进行，在推理过程中的某一步“碰头”
    • (ii) 冲突消解策略
• 三、自然演绎推理
• • 1. 演绎推理（Deductive Reasoning）
  • • (i) 三段论法演绎推理（Syllogistic-Deductive Reasoning）
    • (ii) 假言演绎推理（Hypothetico-Deductive Reasoning）
  • 2. 归纳推理（Inductive Reasoning）
  • 3. 默认推理（Default Reasoning）
  • 4. 自然演绎推理（Natural Deduction）
• 四、归结演绎推理
• • 1. 归结推理的基本思想
  • 2. 谓词逻辑的相关概念
  • 3. 谓词公式化：前束范式（Prenex Normal Form）
  • 4. 斯科伦范式（Skolem Standard Form）
  • 5. 子句（Clause）与子句集
  • 6. 海伯伦（Herbrand）理论
  • 7. 鲁滨逊归结（Resolution）原理（消解原理）
  • • (i) 鲁滨逊归结原理的基本思想
    • (ii) 谓词逻辑的文字互补与置换（Substitution）
    • (iii) 归结反演
    • (iv) 归结原理的问题求解

一、推理基本概念

推理：从已知事实和知识出发，按照某种策略或规则，逐步退出结论或证明某个假设成立或不成立，或者归纳出新事实的思维过程

推理的客观基础：客观事物间的相互关系

推理的两个基本要素：

• 事实/证据：推理的出发点、推理时应该使用的知识
• 知识：使推理得以向前推进，并逐步达到最终目标的依据

在人工智能系统中，推理过程通常由推理机来实现

推理机（inference engine）通常是一组程序，用来控制协调整个系统

推理的形式（论式）：体现前提和结论之间的逻辑联系，任何推理过程都表现为按照一定的推理规则，把前提和结论排列成一定的推理形式；否则，就不是推理

推理必须依靠命题来表达，每种推理形式都有自己的具体要求（即推理规则）

• 推理的内容：前提和结论的命题内容
• 推理的形式：是前提和结论的命题形式之间的连结方式，体现前提和结论之间的逻辑联系

逻辑形式的有效性：凡是从真前提必然得出真结论的推理，就是有效的，否则无效

推理形式不能保证从真前提必然得出真结论，只有内容真实且形式有效的推理才是正确的推理

推理形式的解释：将一个推理形式中的逻辑变项（没有确切含义的符号或词语）置换成具体内容的词项或命题

这个例子中前提是真的，但结论是假的，所以推理形式无效

如果一个推理形式有效，其任何解释都是有效的，但一个推理形式的解释不可穷尽，解释的方法只能判定一个推理是否无效，不能判断一个推理形式必然有效

逻辑形式的可靠性：当且仅当推理是有效的，并且其所有前提是真的时，推理才有效

推理分类：知识的确定性

推理的分类：按逻辑基础

二、推理逻辑基础

1. 命题逻辑（Propositional Logic）

命题逻辑：见这篇文章

补充内容：

1. “我正在撒谎”是悖论，不是命题
   命题：非真即假/将来会知道或证明必是真假
   非命题：不是陈述句/没有做出判断/真假不确定/悖论
2. 原子命题：没有逻辑连接词
3. 连接词运算的优先顺序为¬,∧,∨,→,↔\neg,\land,\lor,\to,\leftrightarrow¬,∧,∨,→,↔

范式（Normal Form）：将命题公式化归为一种标准的形式，其最大的作用是可以进行两个命题的等价判断

• 析取范式（Disjunctive Normal Form, DNF）：有限个简单合取式构成的析取式
• 合取范式（Conjunctive Normal Form, CNF）：有限个简单析取式构成的合取式

范式存在定理：任何命题公式都存在着与之等值的析取范式和合取范式

命题公式的析取范式与合取范式都不是唯一的

命题符号化注意点：

(1) 连接词与日常词汇不完全一致
(2) 命题真假根据定义理解
(3) 不能对号入座（“或”可能是相容或p∨qp\lor qp∨q，也可能是排斥或(p∧¬q)∨(¬p∧q)(p\land\neg q)\lor(\neg p\land q)(p∧¬q)∨(¬p∧q)）
(4) 有些词也可以表示为五个连接词之一（比如“但是”就是合取的意思）

2. 谓词逻辑（Predicate Logic）

（主要内容见离散数学教材，这里只提供补充内容）

个体：命题中的主语，可以是常量、变量、函数
个体常量：张三、李四、aaa、bbb、ccc，etc.
个体变量：xxx、yyy、zzz，etc.

函数中个体变量用个体常量代入后结果仍是个体（属于值域），无真值
谓词中个体变量用个体常量代入后变为命题，函数须嵌入到谓词中

函数：个体→个体
谓词：个体→{0,1}\{0,1\}{0,1}

量词（Quantifier）：表示个体与个体域之间的包含关系

• 全称量词（Universal Quantifier）：对于任意，∀\forall∀
• 存在量词（Existential Quantifier）：存在、有一个，∃\exists∃

约束变元：在量词约束下的变量符号
自由变元：不受量词约束的变量符号

量词的辖域：谓词公式中量词的作用范围
e.g. (∀x)(P(x)∧R(x))‾→(∀x)P(x)‾∧Q(x)(\forall x)\underline{(P(x)\land R(x))}\to(\forall x)\underline{P(x)}\land Q(x)(∀x)(P(x)∧R(x))​→(∀x)P(x)​∧Q(x)，第一个∀x\forall x∀x辖域为P(x)∧R(x)P(x)\land R(x)P(x)∧R(x)，第二个∀x\forall x∀x辖域为P(x)P(x)P(x)

全称量词与存在量词的关系：

1. 否定：
   (∀x)P(x)≡¬(∃x)¬P(x)(\forall x)P(x)\equiv \neg(\exists x)\neg P(x)(∀x)P(x)≡¬(∃x)¬P(x)
   ¬(∀x)P(x)≡(∃x)¬P(x)\neg(\forall x)P(x)\equiv(\exists x)\neg P(x)¬(∀x)P(x)≡(∃x)¬P(x)
2. 自由变元可以在或不在量词的约束范围之内（设BBB为不包含变元的谓词公式）：
   (∀x)(A(x)∨B)≡(∀x)A(x)∨B(\forall x)(A(x)\lor B)\equiv(\forall x)A(x)\lor B(∀x)(A(x)∨B)≡(∀x)A(x)∨B
   (∀x)(A(x)∧B)≡(∀x)A(x)∧B(\forall x)(A(x)\land B)\equiv(\forall x)A(x)\land B(∀x)(A(x)∧B)≡(∀x)A(x)∧B
   (∃x)(A(x)∨B)≡(∃x)A(x)∨B(\exists x)(A(x)\lor B)\equiv(\exists x)A(x)\lor B(∃x)(A(x)∨B)≡(∃x)A(x)∨B
   (∃x)(A(x)∧B)≡(∃x)A(x)∧B(\exists x)(A(x)\land B)\equiv(\exists x)A(x)\land B(∃x)(A(x)∧B)≡(∃x)A(x)∧B
3. 约束变元相同的情况下，量词的运算满足分配律：
   (∀x)(A(x)∧B(x))≡(∀x)A(x)∧(∀x)B(x)(\forall x)(A(x)\land B(x))\equiv(\forall x)A(x)\land(\forall x)B(x)(∀x)(A(x)∧B(x))≡(∀x)A(x)∧(∀x)B(x)
   (∃x)(A(x)∨B(x))≡(∃x)A(x)∨(∃x)B(x)(\exists x)(A(x)\lor B(x))\equiv(\exists x)A(x)\lor(\exists x)B(x)(∃x)(A(x)∨B(x))≡(∃x)A(x)∨(∃x)B(x)

谓词的阶和项：

• 一阶谓词：谓词中的所有个体都是个体常量、变量或函数
• 二阶谓词：谓词中的某个个体本身又是一个一阶谓词
• 高阶谓词依此类推
• 项：描述对象的逻辑表达式，被递归定义为：
  • (1) 单独一个个体（常量和变量符号）是项；
  • (2) 若f(t1,t2,⋯,tn)f(t_1,t_2,\cdots,t_n)f(t1​,t2​,⋯,tn​)是nnn元函数符号，t1,t2,⋯,tnt_1,t_2,\cdots,t_nt1​,t2​,⋯,tn​是项，则f(t1,t2,⋯,tn)f(t_1,t_2,\cdots,t_n)f(t1​,t2​,⋯,tn​)是项
  • (3) 有限次地使用上述规则产生的符号串是项

原子谓词公式（简称原子公式）：由单个为此构成不含任何连接词的命题
若P(t1,t2,⋯,tn)P(t_1,t_2,\cdots,t_n)P(t1​,t2​,⋯,tn​)是nnn元谓词，t1,t2,⋯,tnt_1,t_2,\cdots,t_nt1​,t2​,⋯,tn​是项，则P(t1,t2,⋯,tn)P(t_1,t_2,\cdots,t_n)P(t1​,t2​,⋯,tn​)为原子公式

谓词公式（又称合式公式）：由谓词连接词和原子公式连接起来所构成的用于陈述事实的复杂句子

谓词公式本身不是命题，只有对其命题变项赋值后，它才有真值命题公式；谓词逻辑由原子命题、连接词、量词组成

谓词公式的解释：对命题公式中各个命题的一次真值指派

用谓词公式表示事实的步骤如下：
(1) 定义用谓词和个体，确定每个谓词及个体的确切含义
(2) 根据所要表达的事物或概念，为每个谓词中的变元赋以特定的值
(3) 根据所要表达的知识的语义，用适当的连接词将各个谓词连接起来，形成谓词公式

逻辑等价：如果两个命题PPP和QQQ在所有情况下都具有相同的真假值，则这两个命题在逻辑上等价，一般用≡\equiv≡表示，即P≡QP\equiv QP≡Q
(1) P∨Q≡Q∨PP\lor Q\equiv Q\lor PP∨Q≡Q∨P
(2) P∧Q≡Q∧PP\land Q\equiv Q\land PP∧Q≡Q∧P
(3) (P∧Q)∧R≡P∧(Q∧R)(P\land Q)\land R\equiv P\land(Q\land R)(P∧Q)∧R≡P∧(Q∧R)
(4) (P∨Q)∨R≡P∨(Q∨R)(P\lor Q)\lor R\equiv P\lor(Q\lor R)(P∨Q)∨R≡P∨(Q∨R)
(5) ¬(¬P)≡P\neg(\neg P)\equiv P¬(¬P)≡P
(6) P→Q≡¬Q→¬PP\to Q\equiv\neg Q\to\neg PP→Q≡¬Q→¬P
(7) P→Q≡¬P∨QP\to Q\equiv\neg P\lor QP→Q≡¬P∨Q
(8) P↔Q≡(P→Q)∧(Q→P)P\leftrightarrow Q\equiv(P\to Q)\land(Q\to P)P↔Q≡(P→Q)∧(Q→P)
(9) ¬(P∧Q)≡(¬P)∨(¬Q)\neg (P\land Q)\equiv(\neg P)\lor(\neg Q)¬(P∧Q)≡(¬P)∨(¬Q)
(10) ¬(P∨Q)≡(¬P)∧(¬Q)\neg (P\lor Q)\equiv(\neg P)\land(\neg Q)¬(P∨Q)≡(¬P)∧(¬Q)
(11) P∧(Q∨R)≡(P∧Q)∨(P∧R)P\land(Q\lor R)\equiv(P\land Q)\lor(P\land R)P∧(Q∨R)≡(P∧Q)∨(P∧R)
(12) P∨(Q∧R)≡(P∨Q)∧(P∨R)P\lor(Q\land R)\equiv(P\lor Q)\land(P\lor R)P∨(Q∧R)≡(P∨Q)∧(P∨R)

谓词公式常见的推理原则
设A(x)A(x)A(x)为谓词公式，x,yx,yx,y为变元，aaa为常量符号，则有：
(1) 全称量词消去（Universal Instantiation, UI）：(∀x)A(x)⟹A(y)(\forall x)A(x)\implies A(y)(∀x)A(x)⟹A(y)
(2) 全称量词引入（Universal Generalization, UG）：A(y)⟹(∀x)A(x)A(y)\implies(\forall x)A(x)A(y)⟹(∀x)A(x)
(3) 存在量词消去（Existential Instantiation, EI）：(∃x)A(x)⟹A(a)(\exists x)A(x)\implies A(a)(∃x)A(x)⟹A(a)
(4) 存在量词引入（Existential Generalization, EG）：A(a)⟹(∃x)A(x)A(a)\implies(\exists x)A(x)A(a)⟹(∃x)A(x)

3. 推理的控制策略

推理的控制策略：整个问题求解过程中的知识选择和应用顺序

主要控制策略包括：

• 推理方向
• 冲突消解
• 求解策略
• 搜索策略
• 限制策略

推理方法：推理策略确定后，在具体推理时所要采用的匹配方法或不确定传递算法等

(i) 推理方向

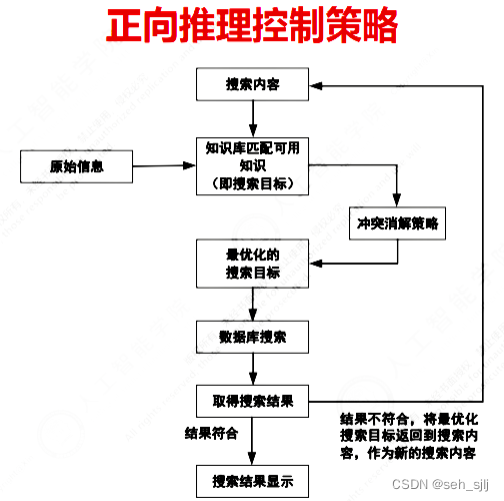
(a) 正向推理：已知事实（条件）→结论

• 推理基本思想
  • 先向综合数据库提供一些初始已知事实，控制系统利用这些数据与知识库中的知识进行匹配，对于被触发的知识，将其结论作为新的事实添加到综合数据库中
  • 重复上述过程，用更新过的综合数据库中的事实再与知识库中另一条知识匹配，将其结论更新至综合数据库中，直到没有可匹配的新知识和不再有新的事实加入到综合数据库中为止
  • 测试是否得到解，有解则返回解，无解则提示运行失败
• 关键：知识与已知事实的匹配方法、知识库的搜索策略
• 优点：推理过程比较直观，允许主动使用有用的事实信息，对用户输入事实做出快速反应，适用于诊断、设计、监控、预测等领域的问题求解
• 缺点：推理无正确目标，搜索范围比较大，求解问题可能会涉及许多与解无关的操作，导致推理效率低

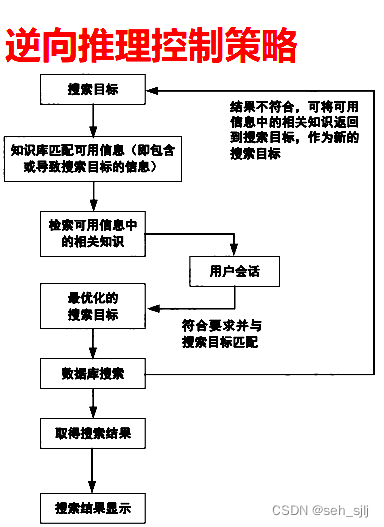
(b) 逆向推理：某个假象目标（结论）→已知条件

主要特点：目标→子目标→子目标→现有条件

• 基本思想:
  • 选定一个假设目标
  • 寻找支持该假设的证据，若所需的证据都能找到，则原假设成立；若无论如何都找不到所需要的证据，说明原假设不成立的；为此需要另作新的假设
• 优点：搜索目标明确，目的性强，不必使用与目标无关的知识，在解空间较小的问题求解环境下尤为合适，在诊断性专家系统中较为有效
• 缺点：初始搜索目标的选择比较自由，对于搜索范围较大，起始目标选择有盲目性，适用于问题空间中有多条途径从初始状态出发，而只有少数路径通向目标状态的问题，否则多次提出假设，影响系统效率

(c) 混合推理：把正向推理和逆向推理结合起来的推理

先正向后逆向：先进行正向推理，帮助选择某个目标，从已知事实演绎出部分结果，再用逆向推理证实该目标或提高其可信度

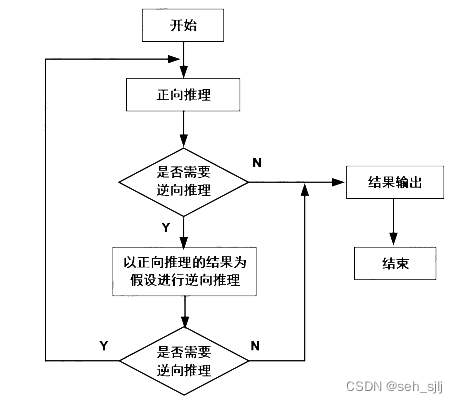
先逆向后正向：先假设一个目标进行逆向推理，然后再利用逆向推理中得到的信息进行正向推理，以退出更多的结论

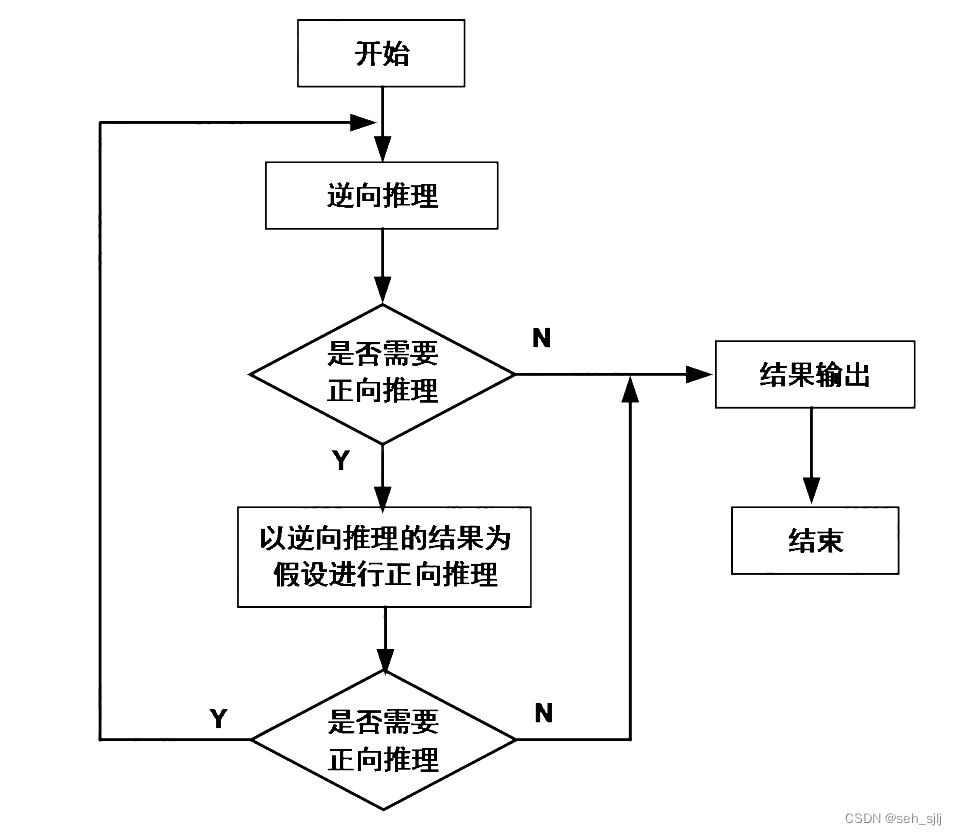
适用的场合：

• 已知事实不够充分
• 由正向推理推出的结论可信度不高
• 希望得出很多其他的结论

(d) 双向推理：正向与逆向推理同时进行，在推理过程中的某一步“碰头”

整个推理过程中，两种推理算法根据一定的控制策略交替运行

(ii) 冲突消解策略

推理冲突：

• 在正向推理中，出现一条事实能与系统知识库中的多条知识匹配，或多个事实与一条知识匹配
• 在逆向推理中，出现同一个假设目标能与系统知识库中多条知识匹配，或多个假设目标能与同一条知识匹配

冲突消解：当推理出现冲突时，需要按一定的策略，在多条冲突的知识中有效地选择一条最合适的知识用于当前推理的解决冲突的过程

冲突消解策略：解决冲突时确定规则的所用顺序

基本思想：对匹配的知识或规则进行排序，以确定匹配知识规则的优先级别

推理冲突经常使用的排序方法有：
(1) 按就近原则排序
(2) 按知识特殊性排序
(3) 按上下文限制排序
(4) 按知识的新鲜性排序
(5) 按知识的差异性排序
(6) 按领域问题的特点排序
(7) 按规则的次序排序
(8) 按前提条件的规模排序

推理的组成和分类

• 组成：前提、结论
• 分类：按逻辑基础、所用的知识、所推出结论的单调性、启发性知识等分类

三、自然演绎推理

1. 演绎推理（Deductive Reasoning）

演绎推理：由已知的普遍性知识或前提出发，通过推导（即“演绎”）得出具体陈述或特殊性结论的推理（即从一般到个别），是自上而下的过程

前提和结论的联系是必然的，是一种确定性推理

演绎推理结论必然为真的两个条件：“前提真实”，“形式有效”

演绎推理不能产生新知识

演绎推理主要包括：三段论、假言推理、选言推理等

(i) 三段论法演绎推理（Syllogistic-Deductive Reasoning）

大前提：普遍原则（e.g. 人都会死）
小前提：特殊事例（e.g. 苏格拉底是人）
结论：肯定结论（e.g. 苏格拉底会死）

三段论的两个基本条件：
(1) 结论必须根据两个前提推演而来，且小前提的主语在概念上不能超出大前提主语概念的范围之外（苏格拉底∈人）
(2) 只有大小两前提所述事实为真时，推理所得结论才会为真，此种前提为真二结论亦为真的推理方式成为有效论证（valid argument）

(ii) 假言演绎推理（Hypothetico-Deductive Reasoning）

大前提（假设，条件）：如果A，那么C（e.g. 如果天下雨，我就带伞）
小前提：A（e.g. 现在天在下雨）
结论：C为真（e.g. 那么，我就带伞）

逻辑形式与三段论类似，但大前提不是一个普遍原则的陈述，而是采取了假设的语气

充分必要条件的性质：

• 肯定前件，就要肯定后件
• 否定前件，就要否定后件
• 肯定后件，就要肯定前件
• 否定后件，就要否定前件

充分条件的性质：

• 肯定前件，就要肯定后件
• 否定后件，就要否定前件

必要条件的性质：

• 肯定后件，就要肯定前件
• 否定前件，就要否定后件

充分条件假言推理：以充分条件的性质作为逻辑推理的依据（如果前件那么后件），前件→后件

必要条件假言推理：以必要条件的性质作为逻辑推理的依据（只有前件才后件，不前件，不后件），后件→前件

充分必要条件假言推理：以充分必要条件的性质作为逻辑推理的依据（前件当且仅当后件）

2. 归纳推理（Inductive Reasoning）

归纳推理：从大量的事例中总结出一般性结论的推理过程，是一种从个别到一般的推理，从特殊的前提推出普遍结论的推理，是自下而上的过程

按照所选事例的广泛性，可分为完全归纳推理、不完全归纳推理

• 完全归纳推理：某种事物全部对象有某种属性→这种事物有该属性，是必然性推理（e.g. 男生都做了核酸，女生也都做了核酸，所以学生都做了核酸）
• 不完全归纳推理：只考察了部分对象就得出了关于该事物的结论，是或然性推理（结论不具有必然性）（e.g. 今年本科生毕业论文抽查没有发现问题，所以，我校今年的本科生毕业沦为都合格）

按照推理所使用的方法，归纳推理可分为枚举归纳、类比归纳、统计归纳、差异归纳

归纳推理没有包含在前提中，是增值知识的过程，归纳推理不全具备必然性

不完全归纳推理分为：

• 简单枚举归纳推理：枚举过程中未遇到相矛盾的情况，依据是经验认知；是或然性推理
  e.g. 铁受热膨胀，铜受热膨胀，铅受热膨胀，……，所以所有金属受热膨胀
• 科学归纳推理：以科学分析为主要依据，由某类中部分对象与其属性之间所具有的因果联系，推出该类的全部对象都具有某种属性
  e.g. 关于生物进化的生存竞争规律

演绎推理与归纳推理的区别：

• 推理的方向不同：一般到个别 vs 个别到一般
• 前提的数量不同：相对有限 vs 不确定
• 结论断定的范围不同：没有超出前提所提供的知识范围 vs 超出
• 前提与结论的联系不同：必然联系 vs 不一定有联系

演绎推理与归纳推理的联系：

• 演绎必须以归纳为基础（演绎推理如果要以一般性知识为前提，那么这些知识通常由归纳推理得出）
• 归纳必须以演绎为指导
• 归纳和演绎推理互相渗透和转化

3. 默认推理（Default Reasoning）

默认推理（即缺省推理）：在知识不完全的情况下作出的推理

通常的形式：如果没有足够的证据证明揭露不成立，则认为结论是正确的

在条件A已成立的情况下，如果没有足够的证据能证明条件B不成立， 则默认B是成立的，并在此默认的前提下进行推理，推导出某个结论

默认推理允许默认某些条件是成立的，摆脱了需要知道全部有关事实才能进行推理的要求，使得在知识不完全的情况下也能进行推理

在默认推理过程中，如果到某一时刻发现原先所作的默认不正确，则就要撤消所作的默认以及由此默认推出的所有结论，重新按新情况进行推理

4. 自然演绎推理（Natural Deduction）

自然演绎推理：从一组已知为真的事实出发，直接运用经典逻辑（命题逻辑、谓词逻辑）中的推理规则，推出结论的过程

假言推理：P,P→Q⟹QP,\,P\to Q\implies QP,P→Q⟹Q
拒取式推理：P→Q,¬Q⟹¬PP\to Q,\,\neg Q\implies\neg PP→Q,¬Q⟹¬P
假言三段论：P→Q,Q→R⟹P→RP\to Q,\,Q\to R\implies P\to RP→Q,Q→R⟹P→R

例 设有如下事实：
(1) 只要是豪车，Musk都喜欢。
(2) 所有价格在一千万元以上的车都是豪车。
(3) 兰博基尼的价格在一千万元以上。
求证：Musk喜欢兰博基尼。

证明：定义谓词
LuxuryCar(x)\text{LuxuryCar}(x)LuxuryCar(x)：xxx是豪车
Like(x,y)\text{Like}(x,y)Like(x,y)：xxx喜欢yyy
Above(x,y)\text{Above}(x,y)Above(x,y)：xxx的价格在yyy元以上
已知事实：
(1) LuxuryCar(x)→Like(Musk,x)\text{LuxuryCar}(x)\to\text{Like}(\text{Musk},x)LuxuryCar(x)→Like(Musk,x)
(2) ∀x(Above(x,TenMillion)→LuxuryCar(x))\forall x(\text{Above}(x,\text{TenMillion})\to\text{LuxuryCar}(x))∀x(Above(x,TenMillion)→LuxuryCar(x))
(3) Above(Lamborghini,TenMillion)\text{Above}(\text{Lamborghini},\text{TenMillion})Above(Lamborghini,TenMillion)
则：
Above(Lamborghini,TenMillion),Above(x,TenMillion)→LuxuryCar(x)⟹LuxuryCar(Lamborghini)\text{Above}(\text{Lamborghini},\text{TenMillion}),\,\text{Above}(x,\text{TenMillion})\to\text{LuxuryCar}(x)\implies\text{LuxuryCar}(\text{Lamborghini})Above(Lamborghini,TenMillion),Above(x,TenMillion)→LuxuryCar(x)⟹LuxuryCar(Lamborghini)（假言推理）
LuxuryCar(Lamborghini),LuxuryCar(x)→Like(Musk,x)⟹Like(Musk,Lamborghini)\text{LuxuryCar}(\text{Lamborghini}),\,\text{LuxuryCar}(x)\to\text{Like}(\text{Musk},x)\implies\text{Like}(\text{Musk},\text{Lamborghini})LuxuryCar(Lamborghini),LuxuryCar(x)→Like(Musk,x)⟹Like(Musk,Lamborghini)（假言推理）
这样就证明了Musk喜欢兰博基尼。

自然演绎推理的特点：

• 优点：
  • 表达定理证明过程自然，易理解
  • 拥有丰富的推理规则，推理过程灵活
  • 便于嵌入领域启发式知识
• 缺点:
  • 易产生组合爆炸，得到的中间结论一般呈指数形式递增
  • 不利于复杂问题的推理,甚至难以实现

四、归结演绎推理

1. 归结推理的基本思想

归结（Resolution）推理：在人工智能，几乎所有问题都可以转化为一个定理证明问题，而定理证明的实质就是要从前提PPP出发推出结论QQQ，即需要证明P→QP\to QP→Q永真

归结原理：基于反证法，证明所证公式会假时会产生矛盾，从而说明所证公式为真
与之相比，自然演绎推理是从已知为真的事实出发，运用经典逻辑的推理规则导出结论

归结演绎推理的思路：反证法思想，证明P→QP\to QP→Q永真即证明P∧¬QP\land\neg QP∧¬Q是不可满足的¬(P→Q)≡¬(¬P∨Q)≡P∧¬Q\neg(P\to Q)\equiv\neg(\neg P\lor Q)\equiv P\land\neg Q ¬(P→Q)≡¬(¬P∨Q)≡P∧¬Q

2. 谓词逻辑的相关概念

永真式（重言式，Taotology）：若谓词公式GGG对非空个体域DDD上的任一解释都取真，则称GGG在DDD上是永真的；若GGG在任何非空个体域上均是永真的，则称GGG永真

谓词公式的可满足（Satisfiable）：对于谓词公式GGG，若至少存在DDD上的一个解释，使公式GGG在此解释下的真值为真，则称公式GGG在DDD上是可满足的

谓词公式的永假式（Contradiction/Unsatisfiable）：若谓词公式GGG对非空个体域DDD上的任一解释都取假，则称GGG在DDD上是永假的，或不可满足的

谓词公式的范式：公式的标准形式，有前束范式、斯科伦范式

3. 谓词公式化：前束范式（Prenex Normal Form）

前束范式：所有量词都非否定地处于公式的最前端，且其辖域都延伸至公式的末端(Q1x1)(Q2x2)⋯(Qnxn)M(x1,x2,⋯,xn)(\color{blue}Q_1\color{black}x_1)(\color{blue}Q_2\color{black}x_2)\cdots(\color{blue}Q_n\color{black}x_n)\color{orange}M(x_1,x_2,\cdots,x_n) (Q1​x1​)(Q2​x2​)⋯(Qn​xn​)M(x1​,x2​,⋯,xn​)其中Qi=∀Q_i=\forallQi​=∀或∃\exists∃，M(x1,x2,⋯,xn)\color{orange}M(x_1,x_2,\cdots,x_n)M(x1​,x2​,⋯,xn​)为母式，即不含量词的谓词公式

说明：

• 不含量词的谓词公式也看作前束范式（n=0n=0n=0）
• 任何一个谓词公式均可与一个前束范式等价，且前束范式不是唯一的

谓词公式化为前束范式的步骤：

• 消去→\to→和↔\leftrightarrow↔连接词
• 减少否定词¬\neg¬的数量及辖域
  (1) 双重否定：¬(¬P)≡P\neg(\neg P)\equiv P¬(¬P)≡P
  (2) 德摩根公式：¬(P∨Q)≡¬P∧¬Q\neg(P\lor Q)\equiv\neg P\land\neg Q¬(P∨Q)≡¬P∧¬Q，¬(P∧Q)≡¬P∨¬Q\neg(P\land Q)\equiv\neg P\lor\neg Q¬(P∧Q)≡¬P∨¬Q
  (3) 量词转换：¬(∀x)P(x)≡(∃x)¬P(x)\neg(\forall x)P(x)\equiv(\exists x)\neg P(x)¬(∀x)P(x)≡(∃x)¬P(x)，¬(∃x)P(x)≡(∀x)¬P(x)\neg(\exists x)P(x)\equiv(\forall x)\neg P(x)¬(∃x)P(x)≡(∀x)¬P(x)
• 否定深入：把否定连接词深入到命题变元和谓词的前面
• 约束易名：运用换名规则和代替规则，将公式中所有变元均用不同的符号表示，使得
  • 所有约束变元的名字都不相同
  • 每个量词都有自己唯一的约束变元
• 量词前移：利用量词辖域的扩张把量词移到前面

例 (∀x)F(x)∨¬(∃x)G(x,y)≡(∀x)F(x)∨(∀x)(¬G(x,y))≡(∀x)F(x)∨(∀z)(¬G(y,z))≡(∀x)(F(x)∨(∀z)(¬G(z,y)))≡(∀x)(∀z)(F(x)∨¬G(z,y))\begin{aligned} &(\forall x)F(x)\lor\neg(\exists x)G(x,y)\\ \equiv&(\forall x)F(x)\lor(\forall x)(\neg G(x,y))\\ \equiv&(\forall x)F(x)\lor(\forall z)(\neg G(y,z))\\ \equiv&(\forall x)(F(x)\lor(\forall z)(\neg G(z,y)))\\ \equiv&(\color{blue}\forall\color{balck}x)(\color{blue}\forall\color{balck}z)\color{orange}(F(x)\lor\neg G(z,y)) \end{aligned}≡≡≡≡​(∀x)F(x)∨¬(∃x)G(x,y)(∀x)F(x)∨(∀x)(¬G(x,y))(∀x)F(x)∨(∀z)(¬G(y,z))(∀x)(F(x)∨(∀z)(¬G(z,y)))(∀x)(∀z)(F(x)∨¬G(z,y))​

4. 斯科伦范式（Skolem Standard Form）

斯科伦范式：前束范式中消去全部存在量词∃\exists∃（前缀仅含全称量词），且母式为合取范式的谓词公式(∀x1)(∀x2)⋯(∀xn)M(x1,x2,⋯,xn)(\color{blue}\forall\color{black}x_1)(\color{blue}\forall\color{black}x_2)\cdots(\color{blue}\forall\color{black}x_n)\color{orange}M(x_1,x_2,\cdots,x_n) (∀x1​)(∀x2​)⋯(∀xn​)M(x1​,x2​,⋯,xn​)谓词公式化为斯科伦范式的步骤：

• 化为前束范式
• 消除存在量词（使用斯科伦函数）
• 将全称量词移到前面，并使量词的辖域包括其后公式的整个部分（即量词前移）
• 将母式化为合取范式（“与”）

消去存在量词∃\exists∃的方法：
设有前束范式(Q1x1)(Q2x2)⋯(Qnxn)M(x1,x2,⋯,xn)(\color{blue}Q_1\color{black}x_1)(\color{blue}Q_2\color{black}x_2)\cdots(\color{blue}Q_n\color{black}x_n)\color{orange}M(x_1,x_2,\cdots,x_n)(Q1​x1​)(Q2​x2​)⋯(Qn​xn​)M(x1​,x2​,⋯,xn​)
令QkQ_kQk​为存在量词∃\exists∃：
(1) 若QkQ_kQk​之前不出现全称量词（k=1k=1k=1或前面都是存在量词）：取一个与母式中所有变量都不相同的新常量（如aaa，称为斯科伦常量）代替母式中的所有xkx_kxk​，并删除前缀中的(∃xk)(\exists x_k)(∃xk​)
(2) 若QkQ_kQk​前面有全称量词，则设这些全称量词为Qk1,Qk2,⋯,QkmQ_{k_1},Q_{k_2},\cdots,Q_{k_m}Qk1​​,Qk2​​,⋯,Qkm​​，此时选取一个与母式中的所有变量/函数都不相同的新函数（如f(xk1,xk2,⋯,xkm)f(x_{k_1},x_{k_2},\cdots,x_{k_m})f(xk1​​,xk2​​,⋯,xkm​​)，称为斯科伦函数）代替母式中的所有xkx_kxk​，并删除前缀中的(∃xk)(\exists x_k)(∃xk​)

例 (∃x)(∀y)((∀z)(P(z)∧¬Q(x,z))→R(x,y,f(a)))⟺(∃x)(∀y)(¬(∀z)(P(z)∧¬Q(x,z))∨R(x,y,f(a)))⟺(∃x)(∀y)((∃z)(¬P(z)∨Q(x,z))∨R(x,y,f(a)))⟺(∃x)(∀y)(∃z)(¬P(z)∨Q(x,z)∨R(x,y,f(a)))⟺(∀y)(∃z)(¬P(z)∨Q(ξ,z)∨R(ξ,y,f(a)))⟺(∀y)(¬P(g(y))∨Q(ξ,g(y))∨R(ξ,y,f(a)))\begin{aligned} &(\exists x)(\forall y)((\forall z)(P(z)\land\neg Q(x,z))\to R(x,y,f(a)))\\ \iff&(\exists x)(\forall y)(\neg(\forall z)(P(z)\land\neg Q(x,z))\lor R(x,y,f(a)))\\ \iff&(\exists x)(\forall y)((\exists z)(\neg P(z)\lor Q(x,z))\lor R(x,y,f(a)))\\ \iff&(\exists x)(\forall y)(\exists z)(\neg P(z)\lor Q(x,z)\lor R(x,y,f(a)))\\ \iff&(\forall y)(\exists z)(\neg P(z)\lor Q(\xi,z)\lor R(\xi,y,f(a)))\\ \iff&(\forall y)(\neg P(g(y))\lor Q(\xi,g(y))\lor R(\xi,y,f(a)))\\ \end{aligned}⟺⟺⟺⟺⟺​(∃x)(∀y)((∀z)(P(z)∧¬Q(x,z))→R(x,y,f(a)))(∃x)(∀y)(¬(∀z)(P(z)∧¬Q(x,z))∨R(x,y,f(a)))(∃x)(∀y)((∃z)(¬P(z)∨Q(x,z))∨R(x,y,f(a)))(∃x)(∀y)(∃z)(¬P(z)∨Q(x,z)∨R(x,y,f(a)))(∀y)(∃z)(¬P(z)∨Q(ξ,z)∨R(ξ,y,f(a)))(∀y)(¬P(g(y))∨Q(ξ,g(y))∨R(ξ,y,f(a)))​注意：一个谓词公式的斯科伦范式不一定与原公式完全等价，但它们的可满足性（Satisfiability）是相同的。

5. 子句（Clause）与子句集

原子公式：不含任何连接词的谓词公式
文字（Literal）：原子谓词公式及其否定；PPP称为正文字，¬P\neg P¬P称为负文字
子句：任何文字的析取式（“或”）；任何文字本身就是子句
空子句：不含任何文字的子句，记为NIL\mathrm{NIL}NIL；空子句不能被任何解释所满足，是永假式
子句集：有子句或空子句构成的集合，其变元受全称量词约束，子句之间具有合取关系

子句集的表示：母式为合取范式α1∧α2∧⋯∧αn\alpha_1\land\alpha_2\land\cdots\land\alpha_nα1​∧α2​∧⋯∧αn​，子句集为S={α1,α2,⋯,αn}S=\{\alpha_1,\alpha_2,\cdots,\alpha_n\}S={α1​,α2​,⋯,αn​}

任何谓词公式都可以通过等价关系和推理规则化为相应的子句集

子句集的求解过程：
(1) 化为斯科伦范式
(2) 消去全称量词（母式中的全部变元均受全称量词的约束，并且全称量词的次序已天关紧要，因此可以省掉全称量词,但剩下的母式仍假设其变元是被全称量词量化的）
(3) 消去合取词（把母式表示成子句集，子句集的每个元素都是一个子句）
(4) 更换变量名称（使任意两个字句中不出现相同的变量名；这个动作不改变公式的真值，因为(∀x)((x∨y)∧(x∨z))≡(∀x)(x∨y)∧(∀x)(x∨z)≡(∀x)(x∨y)∧(∀w)(w∨z)(\forall x)((x\lor y)\land(x\lor z))\equiv(\forall x)(x\lor y)\land(\forall x)(x\lor z)\equiv(\forall x)(x\lor y)\land(\forall w)(w\lor z)(∀x)((x∨y)∧(x∨z))≡(∀x)(x∨y)∧(∀x)(x∨z)≡(∀x)(x∨y)∧(∀w)(w∨z)）

例

子句集SSS的不可满足性：对于任意论域的任何一个解释，子句集SSS中子句不能同时取真

定理：一个谓词公式GGG不可满足，当且仅当其标准子句集SSS不可满足，即GGG和SSS的可满足性相同（GGG和SSS不一定等价）

若要证明P→QP\to QP→Q永真，只需证明G=P∧¬QG=P\land\neg QG=P∧¬Q永假，即S={P,¬Q}S=\{P,\neg Q\}S={P,¬Q}不可满足

6. 海伯伦（Herbrand）理论

本来，证明一个子句集不可满足需要对个体域上的一切解释逐个进行判定；但海伯伦构造了一个特殊的域（海伯伦域，简称H域），他证明了只要对这个特殊域上的一切解释进行判定，就可以确保子句集是否不可满足

设谓词公式GGG的子句集为SSS，则按下述方法构造的个体域HHH，称为公式GGG或子句集SSS的海伯伦域（Herbrand Universe）：
(1) 令H0H_0H0​是SSS中所有个体常量的集合，若SSS中不包含个体常量，则令H0={a}H_0=\{a\}H0​={a}，其中aaa为任意指定的一个个体常量
(2) 令Hi+1=Hi∪{S中函数在Hi上的所有实例}H_{i+1}=H_i\cup\{S\text{中函数在}H_i\text{上的所有实例}\}Hi+1​=Hi​∪{S中函数在Hi​上的所有实例}，即：对于GGG中出现的每个形如f(x1,x2,⋯,xn)f(x_1,x_2,\cdots,x_n)f(x1​,x2​,⋯,xn​)的函数，令其每个变量xjx_jxj​都取遍HiH_iHi​中的所有元素，将得到的结果并入Hi+1H_{i+1}Hi+1​中

例1

例2

7. 鲁滨逊归结（Resolution）原理（消解原理）

(i) 鲁滨逊归结原理的基本思想

海伯伦理论的计算量会呈指数增长，用它来计算不现实

鲁滨逊在海伯伦理论的基础上，对子聚集中的子句做逐次归结来证明子句集的不可满足性（如果子句集中各子句相互矛盾），提出归结原理，成为机器证明基础

基本思想：由谓词逻辑转化的子句集中的子句之间是合取关系，只要有一个子句不满足，则整个子句集不满足；如果一个子句集中包含有空子句，则该子句集一定不可满足

基本方法：检查子句集SSS中是否包含空子句，若包含，则SSS不可满足；若不包含，就在子句集中选择合适的子句进行归结，一旦通过归结得到空子句，就说明SSS是不可满足的

鲁滨逊归结的基本思路：通过归结方法不断扩充判定的子句集，并设法使其包含进指示矛盾（即永假）的子句，从而说明子句集不满足

鲁滨逊归结的基本过程：
(1) 首先把欲证明的结论否定，得到一个扩充的子句集S′S'S′
(2) 设法检验子句集S′S'S′是否含有空子句，若含有空子句，则表明S′S'S′不可满足
(3) 若不含有空子句，则继续使用归结法，在子句集中选择合适的子句进行归结，直到导出空子句或不能继续归结

归结过程：设C1C_1C1​和C2C_2C2​是子句集中的任意两个子句，若C1C_1C1​中的文字L1L_1L1​和C2C_2C2​中的L2L_2L2​互补（例如P(x)P(x)P(x)和¬P(x)\neg P(x)¬P(x)互补），从C1C_1C1​和C2C_2C2​中分别消去L1L_1L1​和L2L_2L2​，并将两个子句余下的部分析取，构成一个新子句C12C_{12}C12​，其中C12C_{12}C12​是C1C_1C1​和C2C_2C2​的归结式，C1,C2C_1,C_2C1​,C2​是C12C_{12}C12​的亲本式

设C1=P∨QC_1=P\lor QC1​=P∨Q，C2=¬P∨RC_2=\neg P\lor RC2​=¬P∨R，则C12=Q∨RC_{12}=Q\lor RC12​=Q∨R

归结的过程就是一种推理规则，这也是归结推理的唯一规则

C1,C2C_1,C_2C1​,C2​为真⟹\implies⟹C12C_{12}C12​为真

设C1,C2∈SC_1,C_2\in SC1​,C2​∈S，S1=S∪{C12}S_1=S\cup\{C_{12}\}S1​=S∪{C12​}，则SSS不可满足当且仅当S1S_1S1​不可满足

没有互补文字的两个子句不能归结

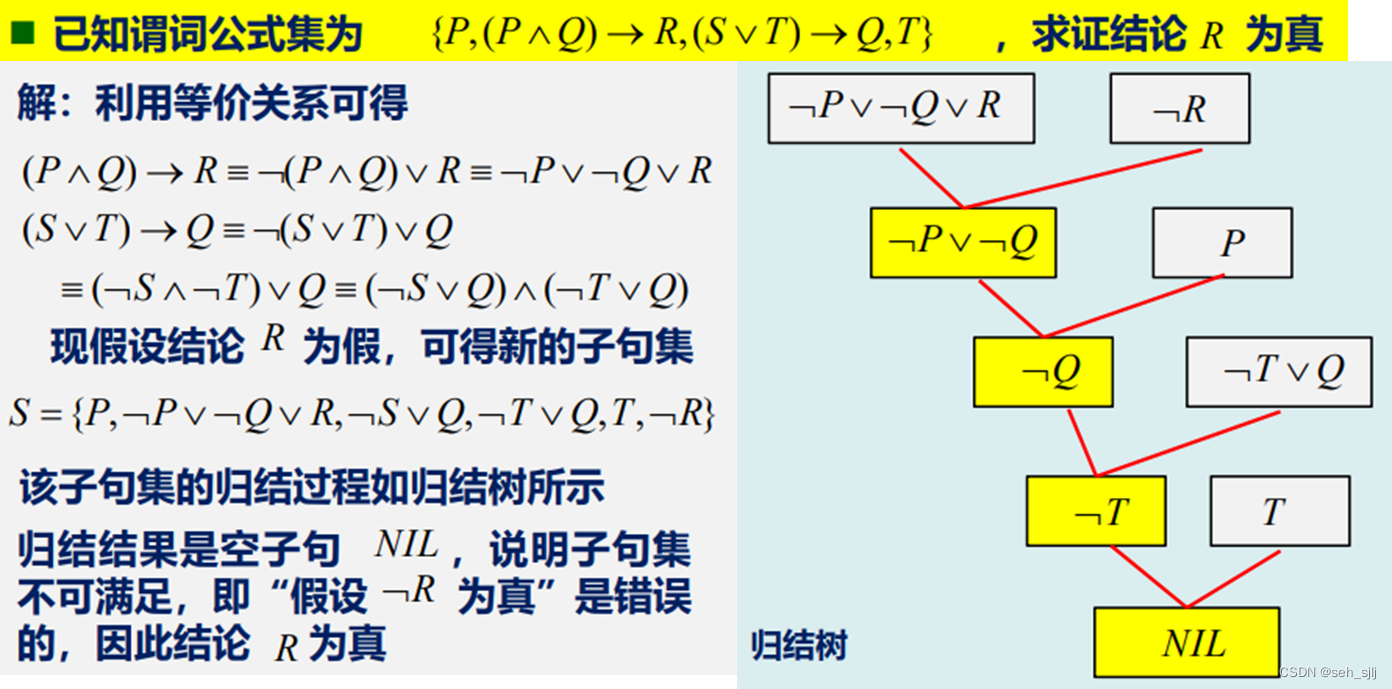
命题逻辑的归结推理示例：

(ii) 谓词逻辑的文字互补与置换（Substitution）

在谓词逻辑中，子句集的谓词子句一般都含有变量，不能直接发现和消去互补文字，文字互补匹配变得复杂

谓词逻辑的归结往往要经过变量置换，然后才能进行归结

置换：用置换项取代子句中的变量，其目的是将某些变量用其他变量、常量或函数替换，使其不再出现

置换形为{t1/x1,t2/x2,⋯,tn/xn}\{t_1/x_1,t_2/x_2,\cdots,t_n/x_n\}{t1​/x1​,t2​/x2​,⋯,tn​/xn​}的有限集合，其中：

• x1,x2,⋯,xnx_1,x_2,\cdots,x_nx1​,x2​,⋯,xn​是互不相同的变量
• t1,t2,⋯,tnt_1,t_2,\cdots,t_nt1​,t2​,⋯,tn​是不同于xix_ixi​的项（可为常量、变量或函数）
• ti/xit_i/x_iti​/xi​：表示用tit_iti​替换xix_ixi​，且tit_iti​和xix_ixi​不能相同，xix_ixi​也不能循环地出现在另一个tit_iti​中

不含任何元素的置换称为空置换，用ε\varepsilonε表示

例：

置换的合成：设有置换σ={t1/x1,t2/x2,⋯,tn/xn}\sigma=\{t_1/x_1,t_2/x_2,\cdots,t_n/x_n\}σ={t1​/x1​,t2​/x2​,⋯,tn​/xn​}，EEE为表达式，则EσE\sigmaEσ表示用项tit_iti​同时置换表达式EEE的所有变量而得到的合成也是一个置换

例：

合一处理：通过多个相对变量的置换，使得两个谓词公式表达一致的过程

设有公式集{E1,E2,⋯,En}\{E_1,E_2,\cdots,E_n\}{E1​,E2​,⋯,En​}，若存在置换σ\sigmaσ，使得E1σ=E2σ=⋯=EnσE_1\sigma=E_2\sigma=\cdots=E_n\sigmaE1​σ=E2​σ=⋯=En​σ，则称σ\sigmaσ为合一置换，{E1,E2,⋯,En}\{E_1,E_2,\cdots,E_n\}{E1​,E2​,⋯,En​}是可合一的

例：

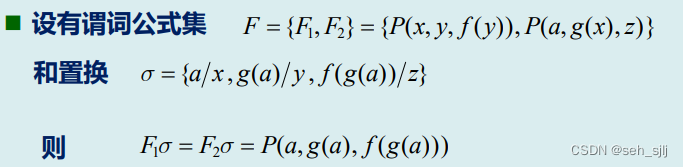
谓词逻辑的归结原理（含变量）：对潜在的互补文字先做变量置换和合一处理，然后才能用于归结

例1：

例2：


为什么这种替换方式是正确的呢？考虑一个简单的例子：从子句P(x)∨Q(y),¬P(z)∨R(w)P(x)\lor Q(y),\neg P(z)\lor R(w)P(x)∨Q(y),¬P(z)∨R(w)推出Q(y)∨R(w)Q(y)\lor R(w)Q(y)∨R(w)。首先化为谓词公式，即：从(∀x)(∀y)(P(x)∨Q(y))∧(∀z)(∀w)(¬P(z)∨R(w))(\forall x)(\forall y)(P(x)\lor Q(y))\land(\forall z)(\forall w)(\neg P(z)\lor R(w))(∀x)(∀y)(P(x)∨Q(y))∧(∀z)(∀w)(¬P(z)∨R(w))推出(∀y)(∀w)(Q(y)∨R(w))(\forall y)(\forall w)(Q(y)\lor R(w))(∀y)(∀w)(Q(y)∨R(w))。对于每个xxx，一定有P(x)∨(∀y)Q(y)P(x)\lor (\forall y)Q(y)P(x)∨(∀y)Q(y)。把zzz代入P(x)∨Q(y)P(x)\lor Q(y)P(x)∨Q(y)即得P(z)∨Q(y)P(z)\lor Q(y)P(z)∨Q(y)。可以把(∀z)(∀w)(¬P(z)∨R(w))(\forall z)(\forall w)(\neg P(z)\lor R(w))(∀z)(∀w)(¬P(z)∨R(w))理解为∀z(P(z)→(∀w)(R(w)))\forall z(P(z)\to(\forall w)(R(w)))∀z(P(z)→(∀w)(R(w)))。那么，对于一个固定的zzz：
➡️如果P(z)=1P(z)=1P(z)=1，则对于任意www，必须有R(w)=1R(w)=1R(w)=1；
➡️如果P(z)=0P(z)=0P(z)=0，则对于任意yyy，必须有Q(y)=1Q(y)=1Q(y)=1，
因此对于每个yyy和www，都有Q(y)∨R(w)Q(y)\lor R(w)Q(y)∨R(w),即(∀y)(∀w)(Q(y)∨R(w))(\forall y)(\forall w)(Q(y)\lor R(w))(∀y)(∀w)(Q(y)∨R(w))。

(iii) 归结反演

要证明P→QP\to QP→Q永真，即证S={P,¬Q}S=\{P,\neg Q\}S={P,¬Q}不可满足。反证法。

归结反演的基本思路：
(1) 将已知前提表示为谓词公式PPP
(2) 将待证明的结论表示为谓词公式QQQ，并否定得到¬Q\neg Q¬Q
(3) 把谓词公式{P,¬Q}\{P,\neg Q\}{P,¬Q}化为子句集SSS
(4) 对子句集SSS进行归结

例1：

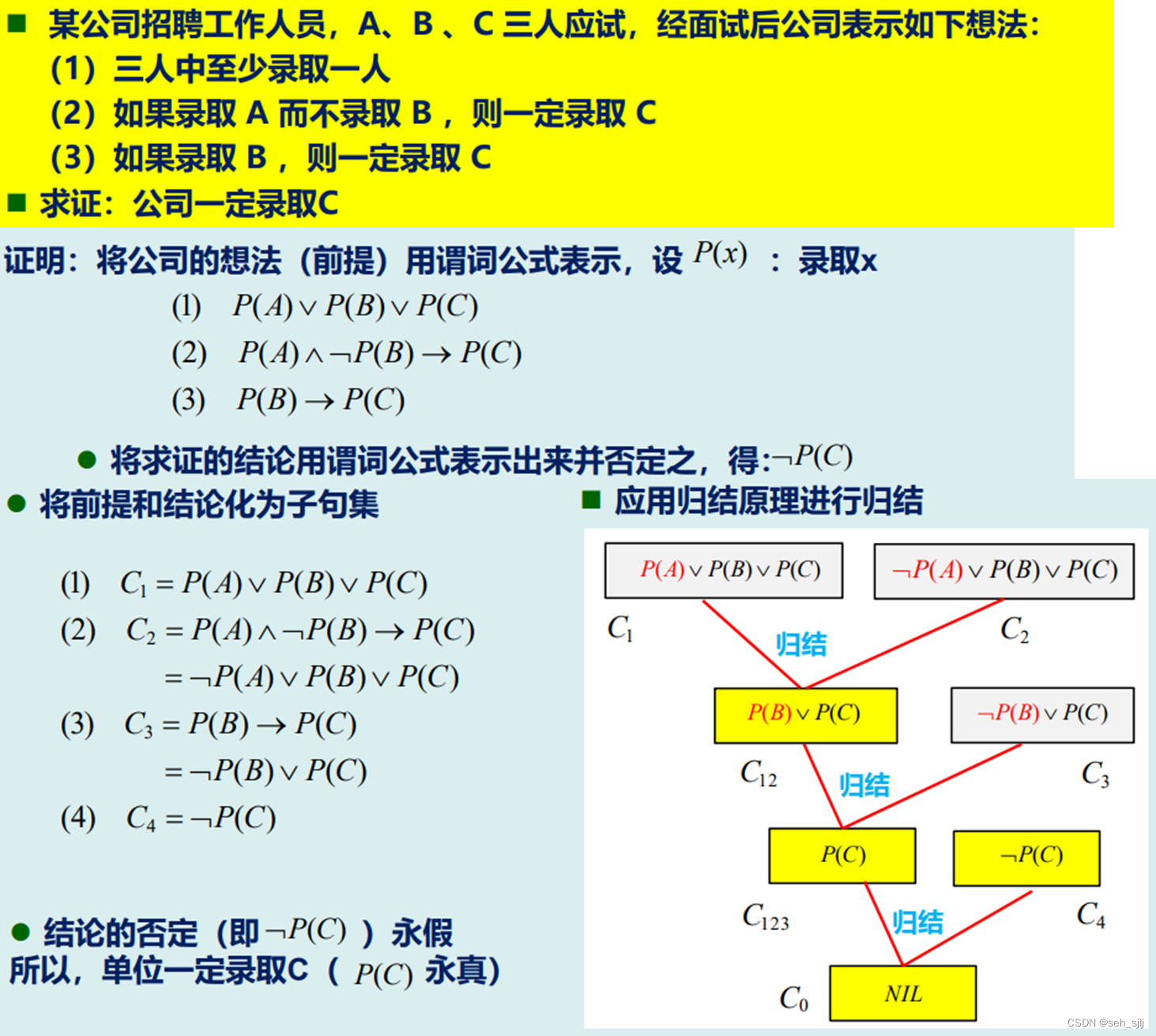
例2：

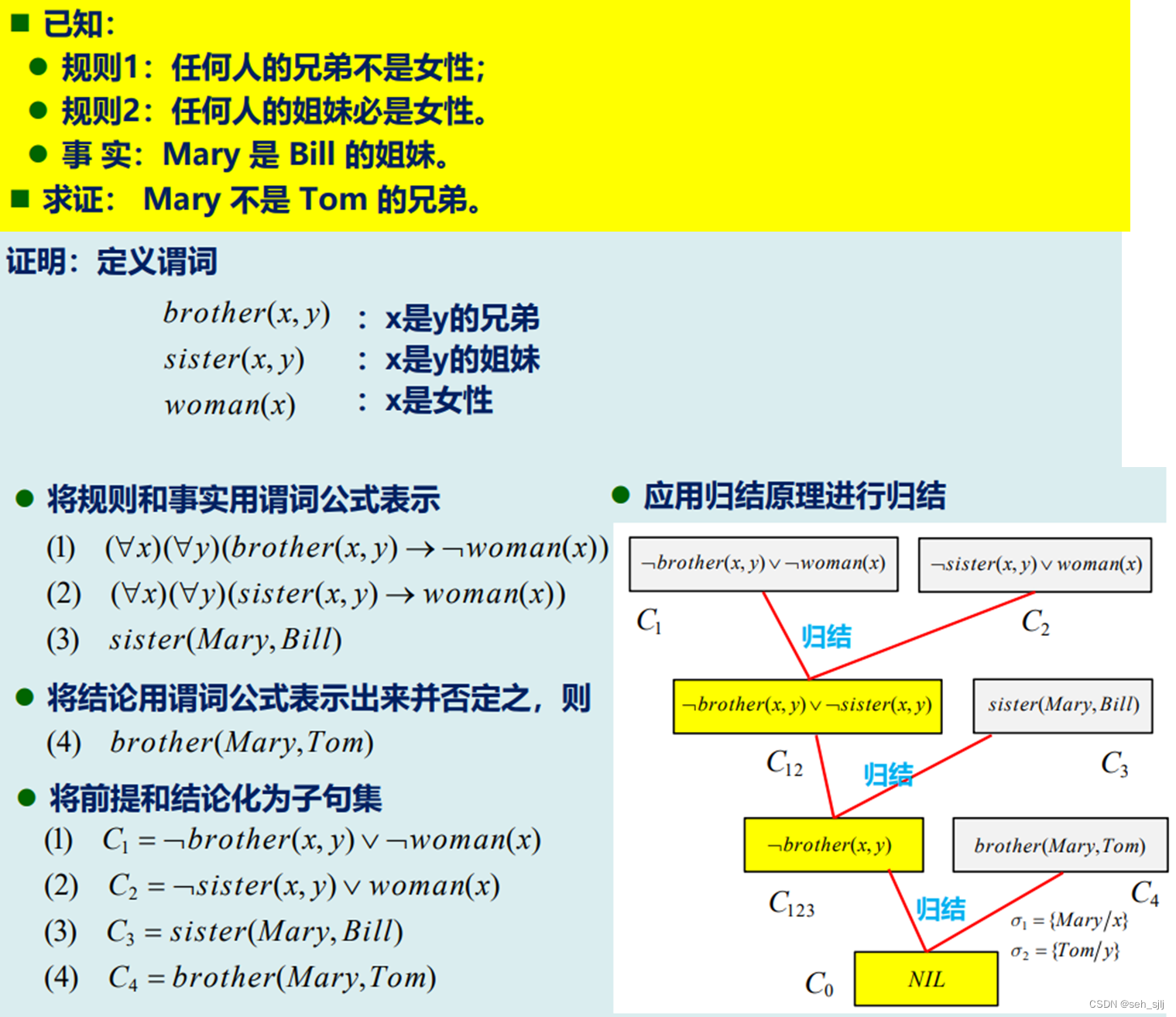
例3：

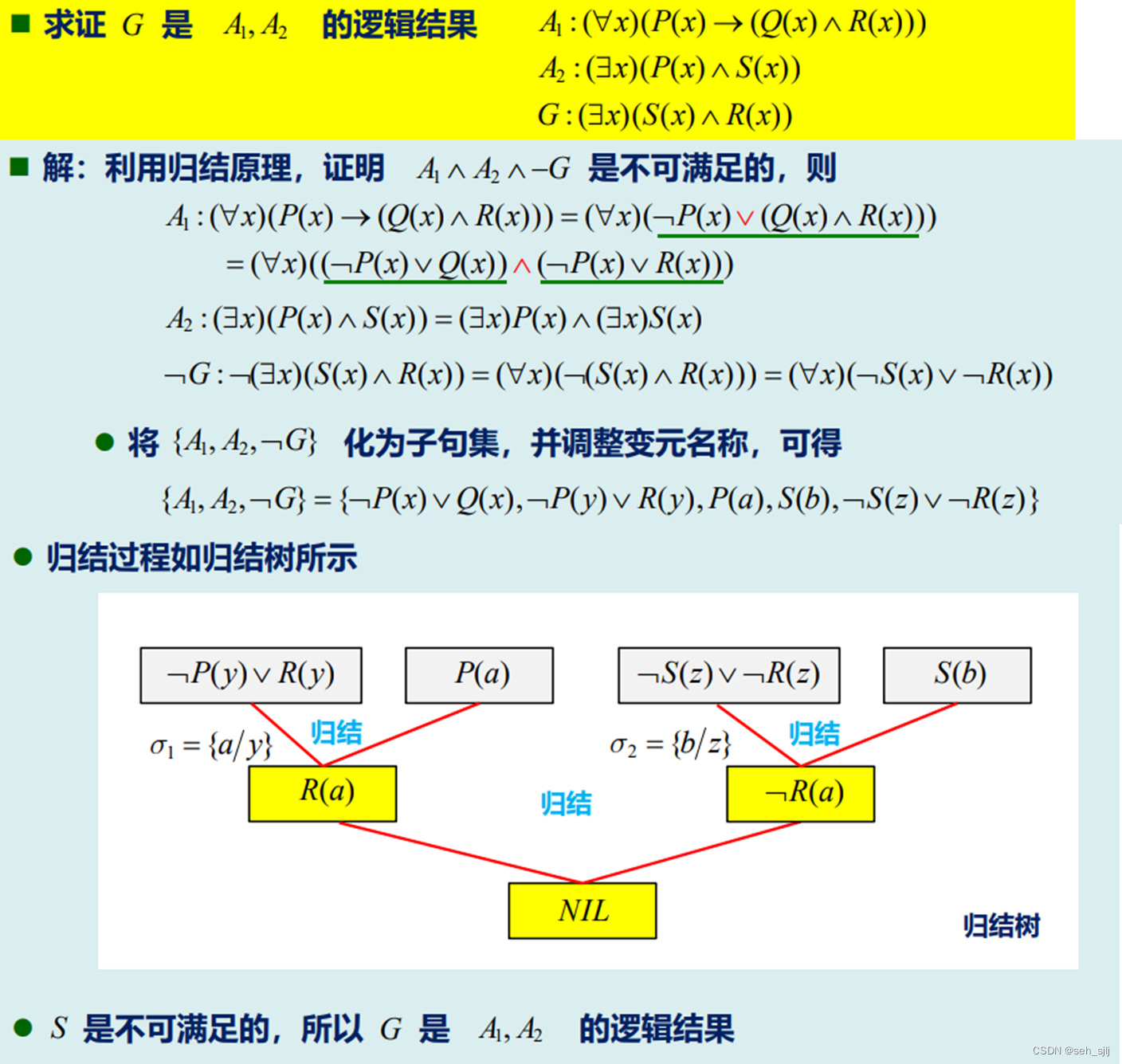
注：求子句集时一定记住不要让不同的子句中出现同一个变量！！！

(iv) 归结原理的问题求解

归结原理既可以用于证明定理，也可以用于获取问题的答案，其思想与证明类似

问题求解的基本步骤：
(1) 将已知前提用谓词公式GGG表示，并化为子句集SSS；
(2) 把待求解的问题用谓词公式QQQ表示，并否定QQQ，再与谓词Answer\text{Answer}Answer构成析取式¬Q∨Answer\neg Q\lor\text{Answer}¬Q∨Answer，其中Answer\text{Answer}Answer是为求解问题而专设的谓词，其变元必须与问题谓词公式的变元一致
(3) 将¬Q∨Answer\neg Q\lor\text{Answer}¬Q∨Answer化为子句集，并加入子句集SSS中，形成新的子句集S′S'S′
(4) 对新的子句集S′S'S′应用归结原理进行归结；
(5) 若得到归结Answer\text{Answer}Answer，则答案就在Answer\text{Answer}Answer中

例：

注：加入的子句等价于Q(x)→Answer(x)Q(x)\to\text{Answer}(x)Q(x)→Answer(x)，即：若xxx满足条件QQQ，那xxx就是问题的答案。这个QQQ就是要问的问题。在上面的例子中，问小张的老师是谁，那么答案xxx满足T(x,Zhang)T(x,\text{Zhang})T(x,Zhang)，所以加入的子句为¬T(x,Zhang)∨Answer(x)\neg T(x,\text{Zhang})\lor\text{Answer}(x)¬T(x,Zhang)∨Answer(x)。