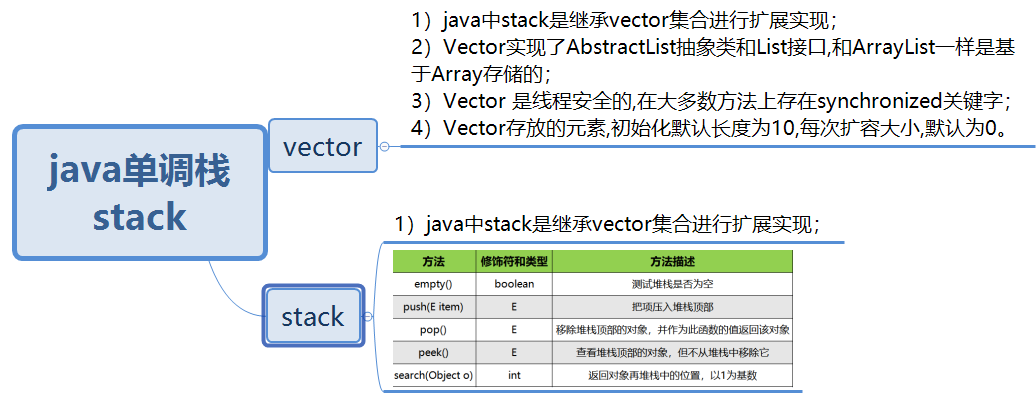
算法刷题入门线性表|单调栈
一、概念
1、栈的定义
栈 是仅限在 一端 进行 插入 和 删除 的 线性表。
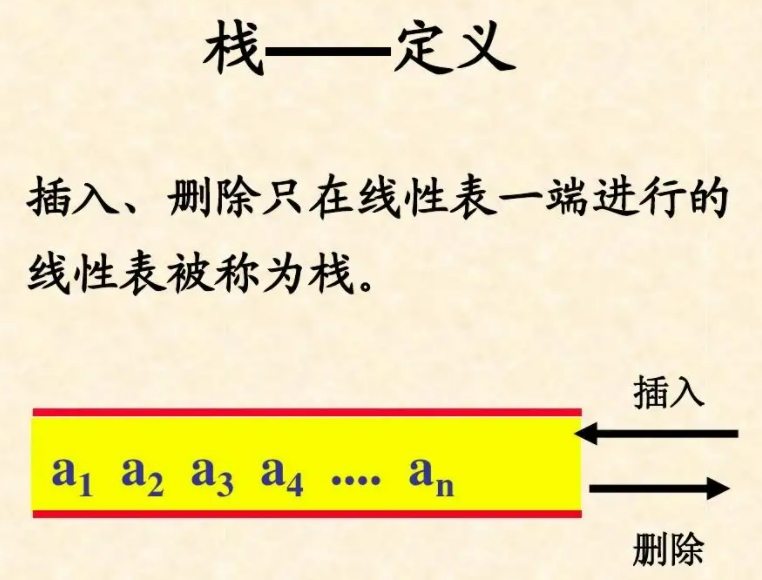
栈 又被称为 后进先出 (Last In First Out) 的线性表,简称 LIFO 。
2、栈顶
栈 是一个线性表,我们把允许 插入 和 删除 的一端称为 栈顶。
3、栈底
和 栈顶 相对,另一端称为 栈底,实际上,栈底的元素我们不需要关心。
二、接口
1、可写接口
1)数据入栈
栈的插入操作,叫做 入栈,也可称为 进栈、压栈。
2)数据出栈
栈的删除操作,叫做 出栈,也可称为 弹栈。
3)清空栈
一直 出栈,直到栈为空。
2、只读接口
1)获取栈顶数据
对于一个栈来说只能获取 栈顶 数据,一般不支持获取 其它数据。
2)获取栈元素个数
栈元素个数一般用一个额外变量存储,入栈 时加一,出栈 时减一。这样获取栈元素的时候就不需要遍历整个栈。通过 O(1) 的时间复杂度获取栈元素个数。
3)栈的判空
当栈元素个数为零时,就是一个空栈,空栈不允许 出栈 操作。
除此之外,单调栈还可以使用队列Deque实现,只要控制只从一端操作数据即可。
补充知识:顺序表和链表
栈可以用 顺序表 实现,也可以用 链表 实现。
(1) 顺序表:顾名思义,将数值按照某种顺序进行存储。按什么顺序呢?其实之所以叫顺序表,是因为该表中的数值都是按照地址大小紧邻着存储,中间不会夹杂任何其他数值的存储方式。那么,只要知道首位元素的位置,顺序表中的任何元素存储位置都可以知道,即:顺序表支持随机访问。
弊端:很明显,因为顺序表数值只能存储在某一块连续的空闲空间里,如果数据很多,该空间存不下,必须要找一个更大的空间存储才可以,否则就会内存溢出。
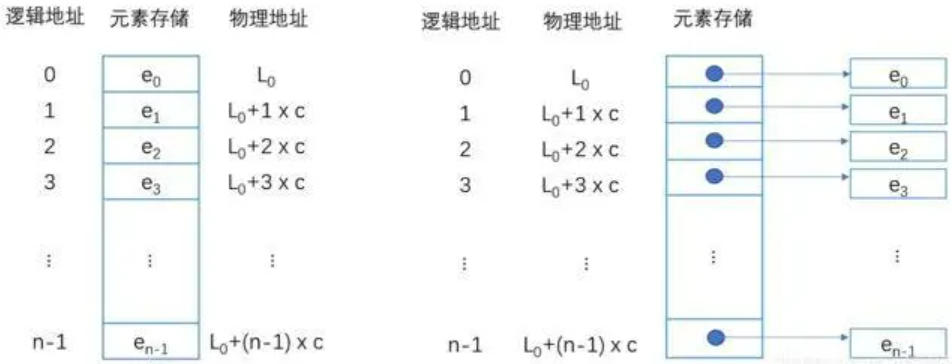
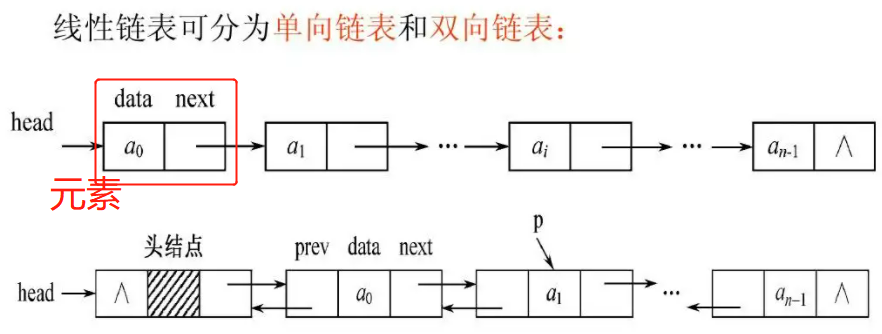
(2) 链表:与顺序表最大的不同点在于,链表存储空间不需要连续。如下图所示,链表中某个元素独立空间存储。那么如何将元素串联起来?从图中可以看到,元素除了有data,还有next(即:指针,用于指向下一个元素的存储的位置,其实它存储的就是下一个元素的位置信息)。
弊端:因为每一个元素都要依赖前一个元素才能知道存储位置,顾无法随机获取某位置上的数据,每次获取数据必须从头开始一个个遍历,直到结尾。
两种方式的优缺点
1、顺序表
在利用顺序表实现栈时,入栈 和 出栈 的常数时间复杂度低,且 清空栈 操作相比 链表实现 能做到 O(1) ,唯一的不足之处是:需要预先申请好空间,而且当空间不够时,需要进行扩容。
2、链表
在利用链表实现栈时,入栈 和 出栈 的常数时间复杂度略高,主要是每插入一个栈元素都需要申请空间,每删除一个栈元素都需要释放空间,且 清空栈 操作是 O(n) 的,直接将 栈顶指针 置空会导致内存泄漏。好处就是:不需要预先分配空间,且在内存允许范围内,可以一直 入栈,没有顺序表的限制。
什么时候可以使用单调栈?
关于使用单调栈的算法题,有一些共同之处:判别是否需要使用单调栈,如果需要找到左边或者右边第一个比当前位置的数大或者小,则可以考虑使用单调栈。
那么关于此类题型,有何模板?
模板如下:
1 public Object formwork(Object T) { //Object可以是任何类型数据,一般为数组2 Stack stack = new Stack<>();3 for (int i = 0; i < T.length; i++) {4 while (!stack.isEmpty() && T[i] > T[stack.peek()]) {//按需处理5 //按需处理6 }7 stack.push(i); //根据需要,选择性入栈8 }9 //返回结果
10 }
题目一:Next Greater Number:
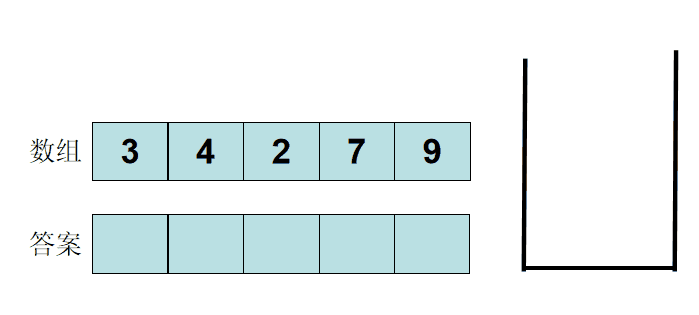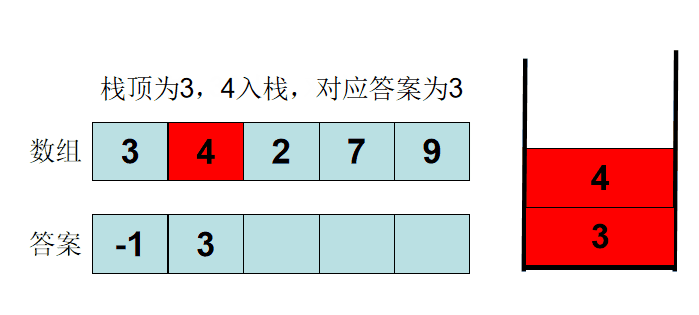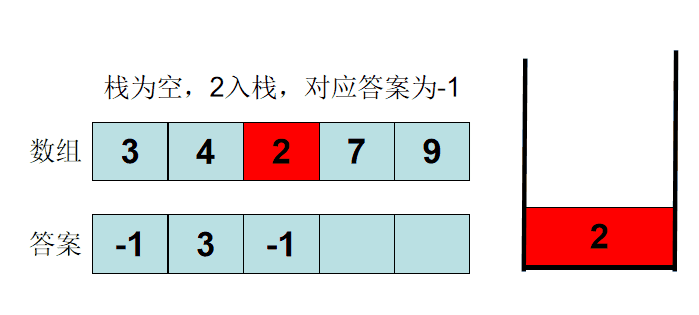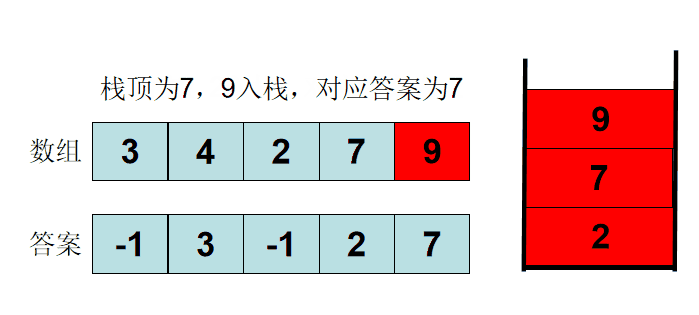
给你⼀个数组, 返回⼀个等⻓的数组, 对应索引存储着下⼀个更⼤元素, 如果没有更⼤的元素, 就存-1。 例⼦:给你⼀个数组 [2,1,5,6,2,3], 你返回数组 [5,5,6,-1,3,-1]。
解释: 第⼀个 2 后⾯⽐ 2 ⼤的数是 5;1 后⾯⽐ 1 ⼤的数是 5; 5 后⾯⽐ 5 ⼤的数是 6; 6后⾯没有⽐ 6 ⼤的数, 填 -1; 第二个2后面比2大的数是3;3 后⾯没有⽐ 3 ⼤的数, 填-1。
也可以这样抽象思考: 把数组的元素想象成并列站⽴的⼈, 元素⼤⼩想象为⼈的⾝⾼。 这些⼈⾯对你站成⼀列, 如何求元素「2」 的 Next GreaterNumber 呢? 很简单, 如果当前人只能抬头往前看,只有比自己高的人才能被看到, ⽐自己矮的人都看不到(因为你是抬头往前看), 那么第⼀个比你高的人身高就是答案。
这道题的暴⼒解法很好想到, 就是对每个元素后⾯都进⾏扫描, 找到第⼀个更⼤的元素就⾏了。 但是暴⼒解法的时间复杂度是 O(n^2)。
单调栈的算法模板
1 public static int[] formwork(int[] T) {2 Stack stack = new Stack<>();3 int[] ret = new int[T.length];4 for (int i = 0; i < T.length; i++) {5 while (!stack.isEmpty() && T[i] > T[stack.peek()]) { //按需处理,包括内部逻辑6 int idx = stack.pop();7 ret[idx] = i - idx;8 }9 stack.push(i);
10 }
11 return ret;
12 }
分析它的时间复杂度, 要从整体来看: 总共有 n 个元素, 每个元素都被push ⼊栈了⼀次, ⽽最多会被 pop ⼀次, 没有任何冗余操作。 所以总的计算规模是和元素规模 n 成正⽐的, 也就是 O(n) 的复杂度。
题目二:每日温度(Leetcode 739)
给定一个整数数组 temperatures ,表示每天的温度,返回一个数组 answer ,其中 answer[i] 是指对于第 i 天,下一个更高温度出现在几天后。如果气温在这之后都不会升高,请在该位置用 0 来代替。
示例 1:
输入: temperatures = [73,74,75,71,69,72,76,73]
输出: [1,1,4,2,1,1,0,0]
示例 2:
输入: temperatures = [30,40,50,60]
输出: [1,1,1,0]
示例 3:
输入: temperatures = [30,60,90]
输出: [1,1,0]
提示:
1 <= temperatures.length <= 105
30 <= temperatures[i] <= 100
解题思路:
1)暴力解题,会存在超时情况。
2)单调栈:
判别是否需要使用单调栈,如果需要找到左边或者右边第一个比当前位置的数大或者小,则可以考虑使用单调栈。
维护一个栈,里面存放温度对应的索引(因为题目中求的是天数,不是温度)。如果栈为空或者栈顶温度大于当前温度,直接入栈;如果栈顶温度小于当前温度,说明当前温度即为栈顶温度要找的温度,出栈后继续比较栈顶温度。
1 /**2 * 每日温度3 * @param T 73, 74, 75, 71, 69, 72, 76, 734 * @return 1, 1, 4, 2, 1, 1, 0, 05 * 思路:单调栈6 */7 public static int[] dailyTemperatures(int[] T) {8 Stack stack = new Stack<>();9 int[] ret = new int[T.length];
10 for (int i = 0; i < T.length; i++) {
11 while (!stack.isEmpty() && T[i] > T[stack.peek()]) {
12 int idx = stack.pop();
13 ret[idx] = i - idx;
14 }
15 stack.push(i);
16 }
17 return ret;
18 }
题目三. 柱状图中最大的矩形(84)
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。求在该柱状图中,能够勾勒出来的矩形的最大面积。
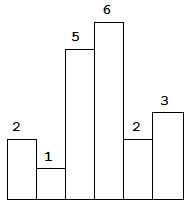
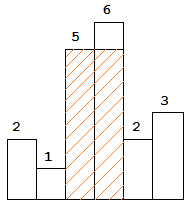
以上是柱状图的示例,其中每个柱子的宽度为 1,给定的高度为 [2,1,5,6,2,3]。图中阴影部分为所能勾勒出的最大矩形面积,其面积为 10 个单位。
输入: [2,1,5,6,2,3]输出: 10
1 /**2 * 柱状图中最大的矩形3 * @param a 2,1,5,6,2,34 * @return 105 */6 public static int largestRectangleArea(int[] a) {7 int max = 0,len =a.length;8 Stack s = new Stack<>();//单调增栈9 for (int i=0; i < len; i++){
10 //当前元素小于栈顶元素时弹栈,直到当前元素大于栈顶元素为止
11 while (!s.isEmpty() && a[i] < a[s.peek()]) {
12 //由于是单调栈,栈中元素都小于等于栈顶,所以可以以栈里当前元素的下标和i的差值作为矩形的宽
13 //因为i实际就是原来栈顶的下标加一
14 int h = a[s.pop()];
15 int dis = s.isEmpty() ? 0 : s.peek() + 1 ;
16 max = Math.max(max, h * (i - dis));
17 }
18 // put current bar's index to the stack
19 s.push(i);
20 }
21 while (!s.isEmpty()) {
22 max = Math.max(max, a[s.pop()] * (len - (s.isEmpty() ? 0 : s.peek() + 1)));
23 }
24 return max;
25 }
题目四. Leetcode 85:最大矩形(难)
题目描述:
给定一个仅包含 0 和 1 的二维二进制矩阵,找出只包含 1 的最大矩形,并返回其面积。
示例:
输入:
[
["1","0","1","0","0"],
["1","0","1","1","1"],
["1","1","1","1","1"],
["1","0","0","1","0"]
]
输出: 6
1 /**2 * LeetCode(85):最大矩形3 * @param matrix4 * [5 * ["1","0","1","0","0"],6 * ["1","0","1","1","1"],7 * ["1","1","1","1","1"],8 * ["1","0","0","1","0"]9 * ]
10 * @return 6
11 * 思路:逐行每列累积汇总,每列为1的高度;每次遇到0元素,该列高度置零
12 * 每行形成的高度数组,按照柱状图中最大的矩形(单调栈)
13 */
14 public static int maximalRectangle(char[][] matrix) {
15 if (matrix == null || matrix.length == 0) return 0;
16 int row = matrix.length; //行数
17 int col = matrix[0].length; //列数
18 int[] height = new int[col];
19 int res = 0;
20 for (int i = 0; i < row; i++) {
21 for (int j = 0; j < col; j++) {
22 if (matrix[i][j] == '1') height[j] += 1; //每列有1,加
23 else height[j] = 0; //每列有0,置空0
24 }
25 res = Math.max(res, largestRectangleArea(height));//每行调用柱状图中最大的矩形方法
26 }
27 return res;
28 }
29
30
31 /**
32 * 柱状图中最大的矩形
33 * @param a 2,1,5,6,2,3
34 * @return 10
35 */
36 public static int largestRectangleArea(int[] a) {
37 int max = 0,len =a.length;
38 Stack s = new Stack<>();//单调增栈
39 for (int i=0; i < len; i++){
40 //当前元素小于栈顶元素时弹栈,直到当前元素大于栈顶元素为止
41 while (!s.isEmpty() && a[i] < a[s.peek()]) {
42 //由于是单调栈,栈中元素都小于等于栈顶,所以可以以栈里当前元素的下标和i的差值作为矩形的宽
43 //因为i实际就是原来栈顶的下标加一
44 int h = a[s.pop()];
45 int dis = s.isEmpty() ? 0 : s.peek() + 1 ;
46 max = Math.max(max, h * (i - dis));
47 }
48 // put current bar's index to the stack
49 s.push(i);
50 }
51 while (!s.isEmpty()) {
52 max = Math.max(max, a[s.pop()] * (len - (s.isEmpty() ? 0 : s.peek() + 1)));
53 }
54 return max;
55 }
题目五. LeetCode 496. 下一个更大元素 I
给定两个没有重复元素的数组 nums1 和 nums2 ,其中nums1 是 nums2 的子集。找到 nums1 中每个元素在 nums2 中的下一个比其大的值。
nums1 中数字 x 的下一个更大元素是指 x 在 nums2 中对应位置的右边的第一个比 x 大的元素。如果不存在,对应位置输出-1。
示例 1:
输入: nums1 = [4,1,2], nums2 = [1,3,4,2].
输出: [-1,3,-1]
解释:
对于num1中的数字4,你无法在第二个数组中找到下一个更大的数字,因此输出 -1。
对于num1中的数字1,第二个数组中数字1右边的下一个较大数字是 3。
对于num1中的数字2,第二个数组中没有下一个更大的数字,因此输出 -1。
示例 2:
输入: nums1 = [2,4], nums2 = [1,2,3,4].
输出: [3,-1]
解释:
对于num1中的数字2,第二个数组中的下一个较大数字是3。
对于num1中的数字4,第二个数组中没有下一个更大的数字,因此输出 -1。
注意:
nums1和nums2中所有元素是唯一的。
nums1和nums2 的数组大小都不超过1000。
思路:利用Map和Stack,找到nums2中每个元素右边比自己大的数,存放到Map中,键存放自身,值存放比自己大的元素,找不到不存放;然后遍历nuns1寻找即可
1 /**2 * 下一个更大元素 I3 * @param nums1 4,1,24 * @param nums2 1,3,4,25 * @return -1,3,-16 */7 public static int[] nextGreaterElement(int[] nums1, int[] nums2) {8 Map map=new HashMap<>();9 Stack stack=new Stack<>();
10 for (int i=0, len= nums2.length; i nums2[stack.peek()]) {
12 map.put(nums2[stack.pop()], nums2[i]);
13 }
14 //先将数据入栈,这里只比较比自己大的值,小的先入栈,或者本身入栈
15 stack.push(i);
16 }
17 //nums1中元素,在map中匹配寻找更大值
18 int num[]=new int[nums1.length];
19 for (int i=0,len=nums1.length;i
题目六. Leetcode 503:下一个更大元素 II
给定一个循环数组(最后一个元素的下一个元素是数组的第一个元素),输出每个元素的下一个更大元素。数字 x 的下一个更大的元素是按数组遍历顺序,这个数字之后的第一个比它更大的数,这意味着你应该循环地搜索它的下一个更大的数。如果不存在,则输出 -1。
示例 1:
输入: [1,2,1]
输出: [2,-1,2]
解释: 第一个 1 的下一个更大的数是 2;
数字 2 找不到下一个更大的数;
第二个 1 的下一个最大的数需要循环搜索,结果也是 2。
注意: 输入数组的长度不会超过 10000。
1 /**2 * Leetcode 503:下一个更大元素 II3 * @param nums 1,2,14 * @return 2,-1,25 */6 public static int[] nextGreaterElements(int[] nums) {7 Stack st = new Stack<>();8 int len = nums.length;9 int[] res = new int[len];
10 Arrays.fill(res,-1); //初始化
11 for(int i = 0 ;i < 2*len; i++){ //存在循环取最大,最多2次遍历
12 //取余,注意2次循环越界问题
13 while(!st.isEmpty() && nums[i % len] > nums[st.peek()]){
14 int x = st.pop();
15 res[x] = nums[i % len];
16 }
17 if(i < len) st.push(i);//注意,只需要第一轮处理即可
18 }
19 return res;
20 }
题目七. Leetcode 901:股票价格跨度
编写一个 StockSpanner 类,它收集某些股票的每日报价,并返回该股票当日价格的跨度。
今天股票价格的跨度被定义为股票价格小于或等于今天价格的最大连续日数(从今天开始往回数,包括今天)。
例如,如果未来7天股票的价格是 [100, 80, 60, 70, 60, 75, 85],那么股票跨度将是 [1, 1, 1, 2, 1, 4, 6]。
示例:
输入:
["StockSpanner","next","next","next","next","next","next","next"], [[],[100],[80],[60],[70],[60],[75],[85]]
输出:[null,1,1,1,2,1,4,6]
解释:
首先,初始化 S = StockSpanner(),然后:
S.next(100) 被调用并返回 1,
S.next(80) 被调用并返回 1,
S.next(60) 被调用并返回 1,
S.next(70) 被调用并返回 2,
S.next(60) 被调用并返回 1,
S.next(75) 被调用并返回 4,
S.next(85) 被调用并返回 6。
注意 (例如) S.next(75) 返回 4,因为截至今天的最后 4 个价格
(包括今天的价格 75) 小于或等于今天的价格。
提示:
1)调用 StockSpanner.next(int price) 时,将有 1 <= price <= 10^5。
2)每个测试用例最多可以调用 10000 次 StockSpanner.next。
3)在所有测试用例中,最多调用 150000 次 StockSpanner.next。
4)此问题的总时间限制减少了 50%。
1 class StockSpanner {2 Stack prices, weights;3 public StockSpanner() { //初始化4 prices = new Stack();5 weights = new Stack();6 }7 public int next(int price) { 8 int w = 1;9 while (!prices.isEmpty() && prices.peek() <= price) {
10 prices.pop();
11 w += weights.pop();
12 }
13 prices.push(price);
14 weights.push(w);
15 return w;
16 }
17 }
题目八.Leetcode 239 滑动窗口最大值
给定一个数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口 k 内的数字。滑动窗口每次只向右移动一位。
返回滑动窗口最大值。
示例:
输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3
输出: [3,3,5,5,6,7]
解释:滑动窗口的位置 最大值
[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7
1 /**2 * Leetcode 239 滑动窗口最大值3 * @param nums 1,3,-1,-3,5,3,6,74 * @param k 35 * @return 3,3,5,5,6,76 */7 public static int[] maxSlidingWindow(int[] nums, int k) {8 if(nums.length<=0){9 return new int[0];
10 }
11 //这里使用的是队列,或者说双向链表都可以
12 Deque windows = new ArrayDeque<>();
13 int[] result = new int[nums.length - k +1]; //数组大小不包括前k-1个,不够窗口
14 for (int i = 0; i < nums.length; i++) {
15 if (i >= k && windows.peekFirst() <= i - k) { //队列中,删除过期数据
16 windows.pollFirst();
17 }
18 //队尾进行比较,比当前值小,剔除
19 while (!windows.isEmpty() && nums[windows.peekLast()] <= nums[i]) {
20 windows.pollLast();
21 }
22 windows.add(i); //当前值下标入队
23 if (i >= k-1) { //下标从0开始,注意判断,赋值
24 result[i - k+1] = nums[windows.peekFirst()];
25 }
26 }
27 return result;
28 }
题目九. Leetcode 962:最大宽度坡
给定一个整数数组 A,坡是元组 (i, j),其中 i < j 且 A[i] <= A[j]。这样的坡的宽度为 j - i。
找出 A 中的坡的最大宽度,如果不存在,返回 0 。
示例 1:
输入:[6,0,8,2,1,5]
输出:4
解释:最大宽度的坡为 (i, j) = (1, 5): A[1] = 0 且 A[5] = 5.
示例 2:
输入:[9,8,1,0,1,9,4,0,4,1]
输出:7
解释:最大宽度的坡为 (i, j) = (2, 9): A[2] = 1 且 A[9] = 1.
提示:
2 <= A.length <= 50000
0 <= A[i] <= 50000
1 /**2 * 最大宽度坡3 * @param a 9,8,1,0,1,9,4,0,4,14 * @return 75 * 最大宽度的坡为 (i, j) = (2, 9): A[2] = 1 且 A[9] = 1.6 */7 public static int maxWidthRamp(int[] a) {8 Stack stack = new Stack<>();9 int ans =0;
10 stack.push(0);
11 //首先进行push,从左向右获取峰谷
12 for (int i=1,len=a.length;i a[i]) {
14 stack.push(i);
15 }
16 }
17 //从右向左进行遍历,获取比较大的值距离
18 for (int i= a.length-1; i>0; i--) {
19 while (!stack.isEmpty() && a[i] >= a[stack.peek()]) {
20 ans = Math.max(ans, i-stack.pop());
21 }
22 }
23 return ans;
24 }
题目十. leetcode 402. 移掉K位数字
题目:
给定一个以字符串表示的非负整数 num,移除这个数中的 k 位数字,使得剩下的数字最小。
注意:
- num 的长度小于 10002 且 ≥ k。
- num 不会包含任何前导零。
示例 1 :
输入: num = "1432219", k = 3
输出: "1219"
解释: 移除掉三个数字 4, 3, 和 2 形成一个新的最小的数字 1219。
示例 2 :
输入: num = "10200", k = 1
输出: "200"
解释: 移掉首位的 1 剩下的数字为 200. 注意输出不能有任何前导零。
示例 3 :
输入: num = "10", k = 2
输出: "0"
解释: 从原数字移除所有的数字,剩余为空就是0。
1 /**2 * 移掉K位数字3 * @param num "1432219"4 * @param k 35 * @return "1219"6 * 思路:先删除前面比较大的值,小的就入栈,删除个数为k;不足k个,就从尾部删除,达到k个7 * 然后进行拼接,去除首位为0的情况8 */9 public static String removeKdigits(String num, int k) {
10 // 遍历,维护一个单调递增栈,如果当前元素比栈顶元素小,并且k>0 则出栈,其余则压栈
11 //可以理解将前面比较大的值去掉(k个),小的入栈
12 Stack stack = new Stack<>();
13 for (int i = 0; i < num.length(); i++) {
14 char c = num.charAt(i);
15 while (!stack.isEmpty() && c < stack.peek() && k > 0) {
16 stack.pop();
17 k--;
18 }
19 stack.push(c);
20 }
21 //如果k>0,说明删除大值个数不满足要求,从栈顶(即数尾)去除,因为前面都是小的了
22 while (k > 0) {
23 stack.pop();
24 k--;
25 }
26 //首位为0去除
27 StringBuilder sb = new StringBuilder();
28 boolean flag = true; //标记首位是否为0
29 for (char c : stack) {
30 if(flag && c =='0') continue; //首位0,不拼接
31 flag = false; //首位有非0
32 sb.append(c); //正常拼接
33 }
34 if (sb.length() ==0) return "0";
35 return sb.toString();
36 }
更多精彩关注wx公众号: