注意力机制目录

• • 输入输出类别（N指向量个数）：
  • Self-attention引入
  • • self-attention架构
    • • self-attention怎么产生bbb
      • • 例子：产生b1b^{1}b1
        • 例子：产生b2b^{2}b2
    • self-attention 总结：
  • Multi-head Self-attention
  • Positional encoding
  • 其他Self-attention应用

输入输出类别（N指向量个数）：

• 第一种：输入 NNN，输出 NNN（例如：Sequence Labeling、POS tagging）
• 第二种：输入 NNN，输出 111（例如：Sentiment analysis）
• 第三种：输入 NNN，输出 N′N'N′（seq2seq任务：由机器自己决定输出的个数）例如：翻译任务、语音辨识

以第一种为例Sequence Labeling任务：

例子： I saw a saw

序列输入到FC层得到各个单词的词性不能解决saw是不同词性的问题，采用考虑上下文的context，将前后几个向量串起来输入到FC，考虑Window包括多个前后多个frame

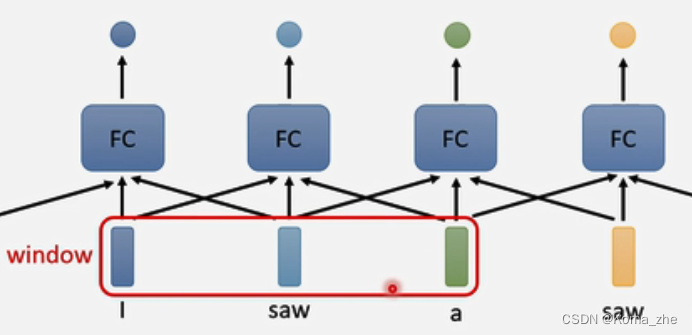
考虑整个input的sequence资讯，可将Window变大甚至盖住整个sequence，但是可能过拟合，FC参数过多。

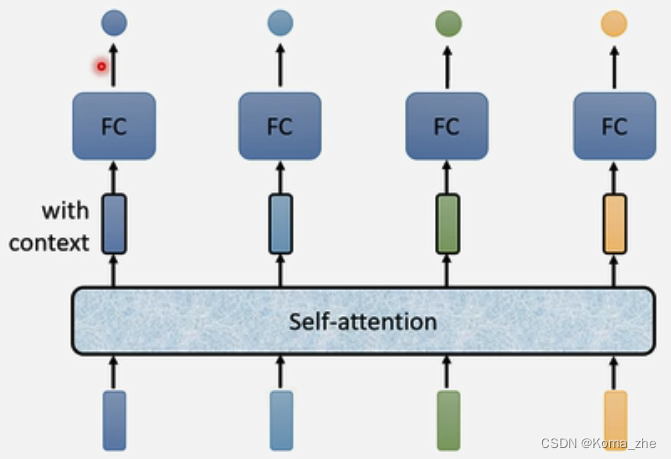
Self-attention引入

考虑整个input的sequence资讯信息更好的办法：
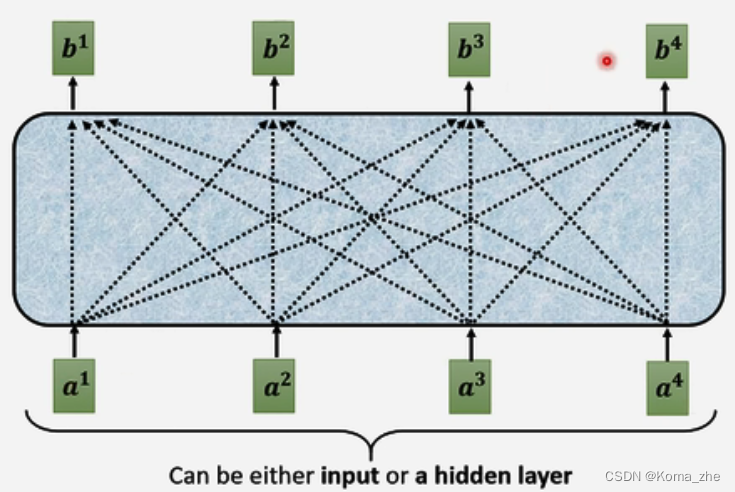
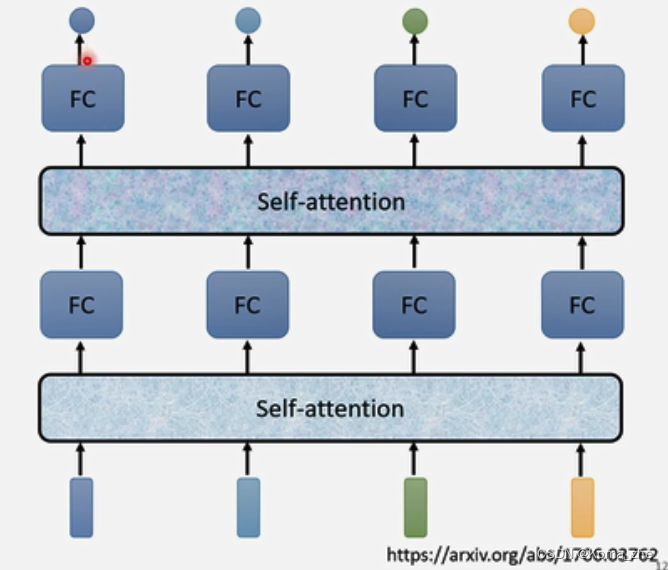
self-attention考虑一整个资讯信息并返回与输入相同数目的vetor输出，再输入FC决定应该是什么。

self-attention可以叠加：
输入+self-attention+FC+self-attention+FC（交替使用，FC专注某一位置的咨询，self-attention关注整个资讯）

注：self-attention最相关文章：Attention is all you need.（提出了transformer，transformer最重要的module就是self-attention，Bert也有应用）

self-attention架构

self-attention输入是一串Vector（可能整个网络的input，也可能是隐层的output）

例：
输入： a1a2a3a4a^{1} \quad a^{2} \quad a^{3} \quad a^{4}a1a2a3a4
输出： b1b2b3b4b^{1} \quad b^{2} \quad b^{3} \quad b^{4}b1b2b3b4

self-attention怎么产生bbb

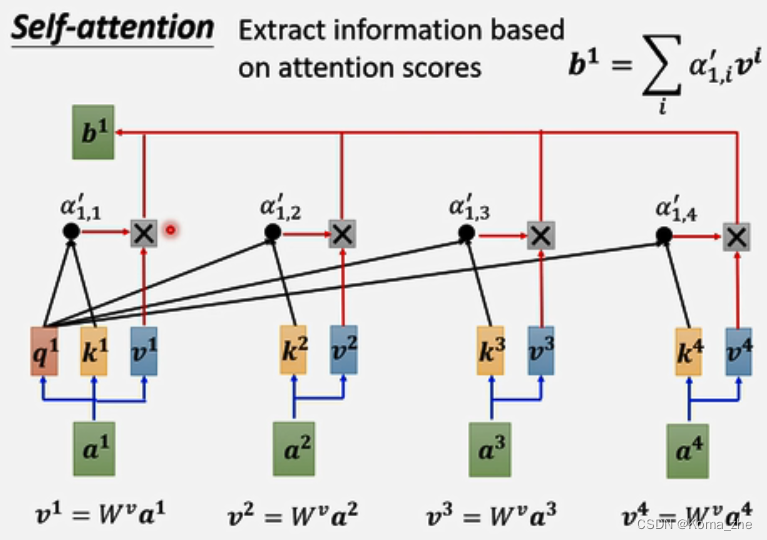
例子：产生b1b^{1}b1

找出与 a1a^{1}a1 相关的其他向量（哪些向量是重要的，哪些部分跟判断 a1a^{1}a1 是哪一个level有关系，哪些是决定 a1a^{1}a1 得class或regression数值所需用到的资讯）
其中每一个向量与 a1a^{1}a1 关联的程度，用数值 α 表示（计算 α 方法有：Dot-product（transformer中使用）、Additive）

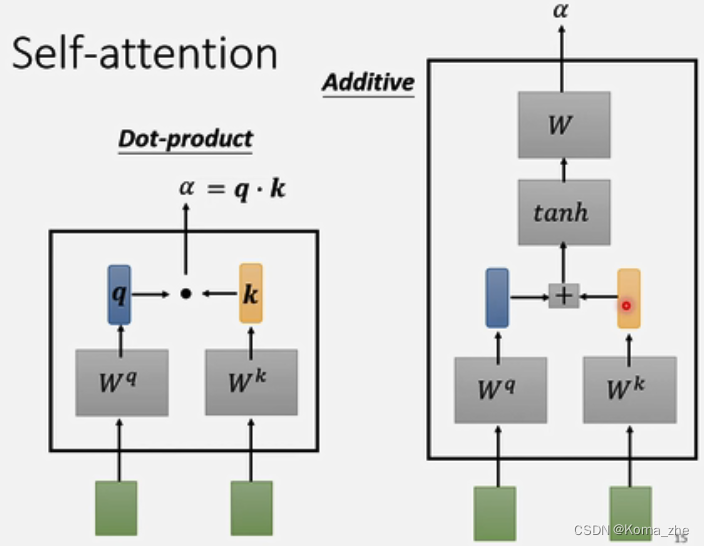
q1=Wqa1q^{1}=W^qa^1q1=Wqa1（qqq称为query）
k2=Wka2k^{2}=W^ka^2k2=Wka2（kkk称为key），k3=Wka3k^{3}=W^ka^3k3=Wka3， k4=Wka4k^{4}=W^ka^4k4=Wka4，k1=Wka1k^{1}=W^ka^1k1=Wka1

α(1,2)=q1⋅k2α(1,2)=q^1·k^2α(1,2)=q1⋅k2（α(1,2)α(1,2)α(1,2)代表query是1提供，key是2提供的，1与2的关联性，也称为attention score），α(1,3)=q1⋅k3α(1,3)=q^1·k^3α(1,3)=q1⋅k3，α(1,4)=q1⋅k4α(1,4)=q^1·k^4α(1,4)=q1⋅k4

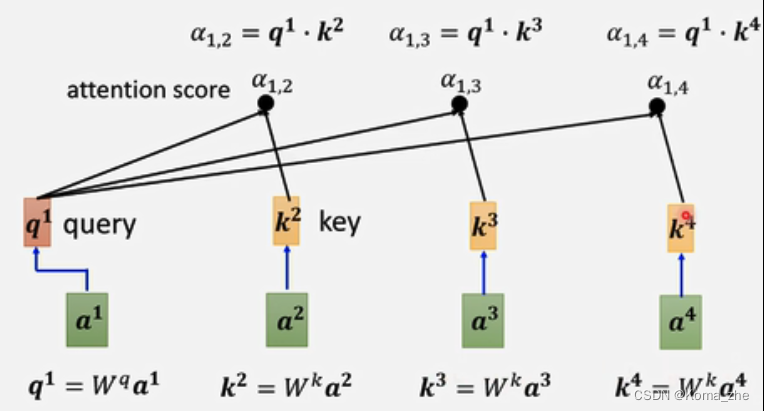
本身也会计算：
α(1,1)=q1⋅k1α(1,1)=q^1·k^1α(1,1)=q1⋅k1
计算出a1a^{1}a1与每一个向量关联性后，做一个softmax，输出一排α′(1,i)α'(1,i)α′(1,i)

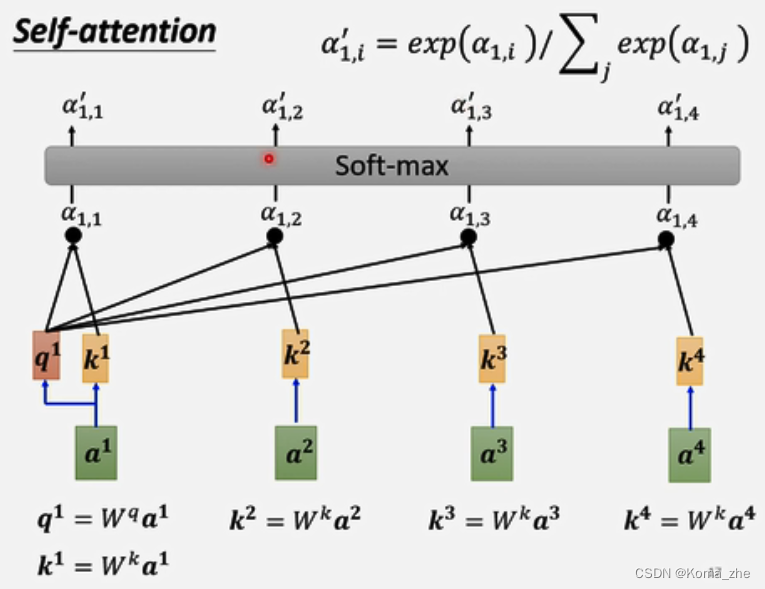
根据 α′α'α′ 抽取这个sequence里重要的咨询：
v1=Wva1v^{1}=W^va^1v1=Wva1、v2=Wva2v^{2}=W^va^2v2=Wva2、v3=Wva3v^{3}=W^va^3v3=Wva3、v4=Wva4v^{4}=W^va^4v4=Wva4
再用 viv^ivi 乘以 α′(1,i)α'(1,i)α′(1,i) ，然后再累加得到 b1b^1b1
α′(1,1)⋅v1+α′(1,2)⋅v2+α′(1,3)⋅v3+α′(1,4)⋅v4=b1α'(1,1)·v^1+α'(1,2)·v^2+α'(1,3)·v^3+α'(1,4)·v^4=b^1α′(1,1)⋅v1+α′(1,2)⋅v2+α′(1,3)⋅v3+α′(1,4)⋅v4=b1

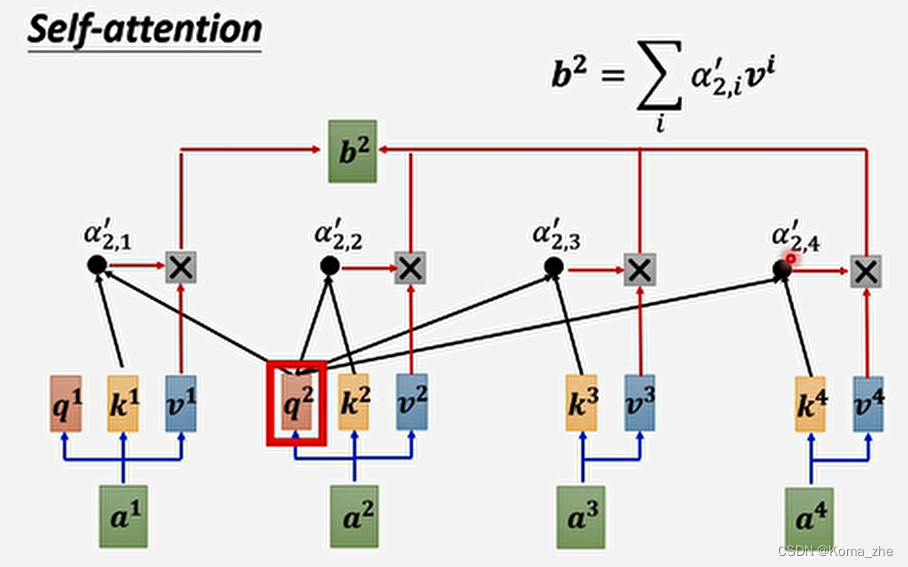
例子：产生b2b^{2}b2

主角：a2a^{2}a2
每一个向量与a2a^{2}a2关联的程度，用数值 ααα 表示（计算 ααα 方法：Dot-product）
q2=Wqa2q^{2}=W^qa^2q2=Wqa2
k1=Wka1k^{1}=W^ka^1k1=Wka1、k2=Wka2k^{2}=W^ka^2k2=Wka2、k3=Wka3k^{3}=W^ka^3k3=Wka3、k4=Wka4k^{4}=W^ka^4k4=Wka4
根据 q2q^{2}q2 去对 a1a1a1 到 a4a4a4 求attention score
α(2,1)=q2⋅k1α(2,1)=q^2·k^1α(2,1)=q2⋅k1、α(2,2)=q2⋅k2α(2,2)=q^2·k^2α(2,2)=q2⋅k2、α(2,3)=q2⋅k3α(2,3)=q^2·k^3α(2,3)=q2⋅k3、α(2,4)=q2⋅k4α(2,4)=q^2·k^4α(2,4)=q2⋅k4
计算出 a2a^{2}a2 与每一个向量关联性后，做一个softmax，输出一排 α′(2,i)α'(2,i)α′(2,i)
根据 α′α'α′ 抽取这个sequence里重要的咨询：
v1=Wva1v^{1}=W^va^1v1=Wva1、v2=Wva2v^{2}=W^va^2v2=Wva2、v3=Wva3v^{3}=W^va^3v3=Wva3、v4=Wva4v^{4}=W^va^4v4=Wva4
再用 viv^ivi 乘以 α′(2,i)α'(2,i)α′(2,i)，然后再累加得到 b2b^2b2
α′(2,1)⋅v1+α′(2,2)⋅v2+α′(2,3)⋅v3+α′(2,4)⋅v4=b2α'(2,1)·v^1+α'(2,2)·v^2+α'(2,3)·v^3+α'(2,4)·v^4=b^2α′(2,1)⋅v1+α′(2,2)⋅v2+α′(2,3)⋅v3+α′(2,4)⋅v4=b2

self-attention 总结：

第一步：每一个a都要分别产生q k v ，I为Input

qi=Wqaiq^{i}=W^qa^iqi=Wqai ——> (q1q2q3q4)=Wq(a1a2a3a4)\begin{pmatrix}q^1&q^2&q^3&q^4\end{pmatrix}=W^q\begin{pmatrix}a^1&a^2&a^3&a^4\end{pmatrix}(q1​q2​q3​q4​)=Wq(a1​a2​a3​a4​)——> Q=Wq⋅IQ=W^q·IQ=Wq⋅I

ki=Wkaik^{i}=W^ka^iki=Wkai——> (k1k2k3k4)=Wk(a1a2a3a4)\begin{pmatrix}k^1&k^2&k^3&k^4\end{pmatrix}=W^k\begin{pmatrix}a^1&a^2&a^3&a^4\end{pmatrix}(k1​k2​k3​k4​)=Wk(a1​a2​a3​a4​)——> K=Wk⋅IK=W^k·IK=Wk⋅I

vi=Wvaiv^{i}=W^va^ivi=Wvai——> (v1v2v3v4)=Wv(a1a2a3a4)\begin{pmatrix}v^1&v^2&v^3&v^4\end{pmatrix}=W^v\begin{pmatrix}a^1&a^2&a^3&a^4\end{pmatrix}(v1​v2​v3​v4​)=Wv(a1​a2​a3​a4​)——> V=Wv⋅IV=W^v·IV=Wv⋅I

第二步：每一个 qiq^{i}qi 都和每一个 kkk 计算 Dot-product 得到 attention score

α(1,1)=k1⋅q1α(1,1) = k^1·q^1α(1,1)=k1⋅q1，α(1,2)=k2⋅q1α(1,2) = k^2·q^1α(1,2)=k2⋅q1，α(1,3)=k3⋅q1α(1,3) = k^3·q^1α(1,3)=k3⋅q1，α(1,4)=k4⋅q1α(1,4) = k^4·q^1α(1,4)=k4⋅q1

α(1,i)=ki⋅q1α(1,i) = k^i·q^1α(1,i)=ki⋅q1 ——> (k1k2k3k4)⋅q1=(α(1,1)α(1,2)α(1,3)α(1,4))\begin{pmatrix}k^1\\k^2\\k^3\\k^4\end{pmatrix}·q^1=\begin{pmatrix}α(1,1)\\α(1,2)\\α(1,3)\\α(1,4)\end{pmatrix}⎝⎜⎜⎛​k1k2k3k4​⎠⎟⎟⎞​⋅q1=⎝⎜⎜⎛​α(1,1)α(1,2)α(1,3)α(1,4)​⎠⎟⎟⎞​

(k1k2k3k4)⋅(q1q2q3q4)=(α(1,1)α(2,1)α(3,1)α(4,1)α(1,2)α(2,2)α(3,2)α(4,2)α(1,3)α(2,3)α(3,3)α(4,3)α(1,4)α(2,4)α(3,4)α(4,4))\begin{pmatrix}k^1\\k^2\\k^3\\k^4\end{pmatrix}·\begin{pmatrix}q^1q^2q^3 q^4\end{pmatrix}=\begin{pmatrix}α(1,1)α(2,1)α(3,1)α(4,1)\\α(1,2)α(2,2)α(3,2)α(4,2)\\α(1,3)α(2,3)α(3,3)α(4,3)\\α(1,4)α(2,4)α(3,4)α(4,4)\end{pmatrix}⎝⎜⎜⎛​k1k2k3k4​⎠⎟⎟⎞​⋅(q1q2q3q4​)=⎝⎜⎜⎛​α(1,1)α(2,1)α(3,1)α(4,1)α(1,2)α(2,2)α(3,2)α(4,2)α(1,3)α(2,3)α(3,3)α(4,3)α(1,4)α(2,4)α(3,4)α(4,4)​⎠⎟⎟⎞​ ——>KT⋅Q=AK^T ·Q=AKT⋅Q=A ——> A′=softmax(A)或Relu(A)A'=softmax(A)或Relu(A)A′=softmax(A)或Relu(A)

第三步：输出 b1=α′(1,i)⋅vib^{1}=α'(1,i)·v^ib1=α′(1,i)⋅vi

(v1v2v3v4)⋅(α(1,1)α(2,1)α(3,1)α(4,1)α(1,2)α(2,2)α(3,2)α(4,2)α(1,3)α(2,3)α(3,3)α(4,3)α(1,4)α(2,4)α(3,4)α(4,4))=(b1b2b3b4)\begin{pmatrix}v^1v^2v^3 v^4\end{pmatrix}·\begin{pmatrix}α(1,1)α(2,1)α(3,1)α(4,1)\\α(1,2)α(2,2)α(3,2)α(4,2)\\α(1,3)α(2,3)α(3,3)α(4,3)\\α(1,4)α(2,4)α(3,4)α(4,4)\end{pmatrix}=\begin{pmatrix}b^1b^2b^3 b^4\end{pmatrix}(v1v2v3v4​)⋅⎝⎜⎜⎛​α(1,1)α(2,1)α(3,1)α(4,1)α(1,2)α(2,2)α(3,2)α(4,2)α(1,3)α(2,3)α(3,3)α(4,3)α(1,4)α(2,4)α(3,4)α(4,4)​⎠⎟⎟⎞​=(b1b2b3b4​)——>V⋅A′=OV·A'=OV⋅A′=O

OOO 其中每一个column就是self-attention的输出。

self-attention中唯一需要学的参数：WqW^qWq、WkW^kWk、WvW^vWv

Multi-head Self-attention

self-attention是用 qqq 去找相关的 kkk ，相关有很多种不同的形式，也许不能只有一个 qqq，要多个 qqq负责不同种类的相关性。
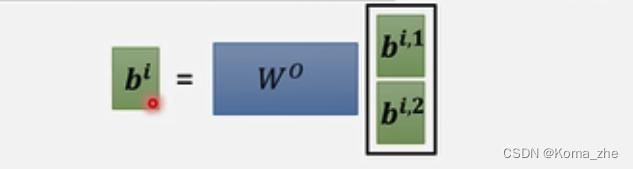
qi=Wqaiq^i=W^qa^iqi=Wqai（qqq称为query）然后 qiq^iqi 再乘以另外2个矩阵得到qi,1q^{i,1}qi,1，qi,2q^{i,2}qi,2
解释：2个head，里面有2种不同相关性，iii代表位置，1和2代表这个位置的第几个qqq，qqq有2个，对应 kkk 和 vvv 也有2个。


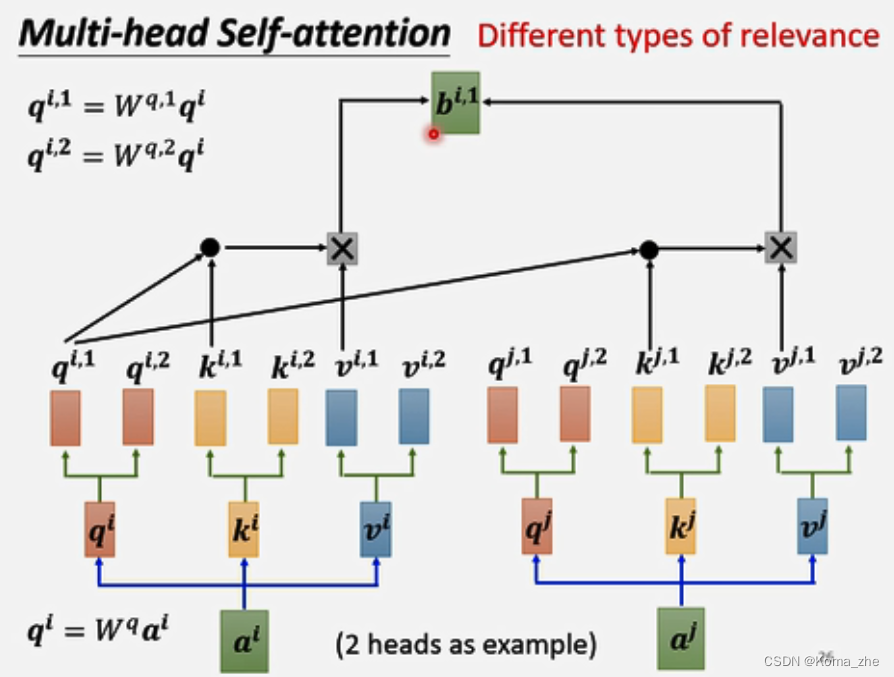
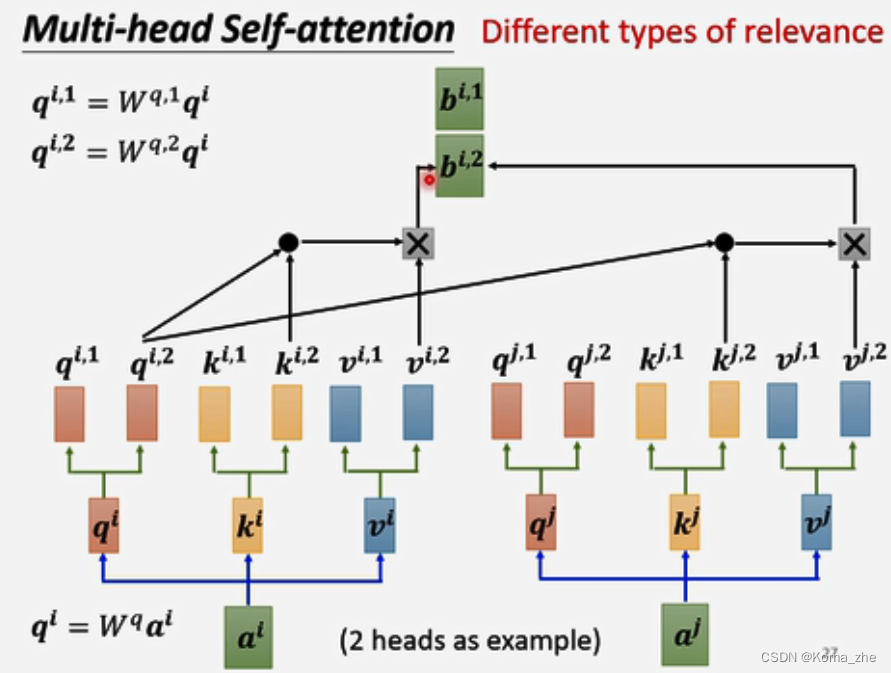
得到的 bbb可以都接起来，再乘以一个矩阵得到 bib^ibi，再送到下一层。

Positional encoding

以上Self-attention的方法没有对位置信息考虑，需要考虑上位置的咨询。
Positional encoding：为每一个位置设定一个vetor（称为positional vetor：eie^iei（iii代表位置）
ei+aie^i + a^iei+ai 再计算 qiq^iqi、kik^iki、viv^ivi

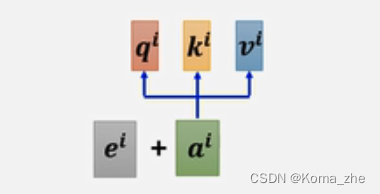
Positional encoding有不同的方法产生：例如sinusiodal/cos、RNN、Floater network、或者通过学习得到。

其他Self-attention应用

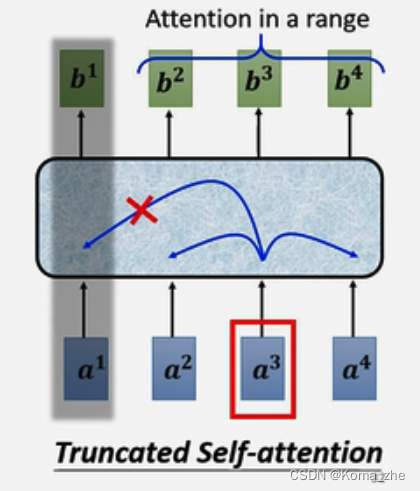
注：做语音识别、语音辨识整个sequence可能太长，使用Truncated Self-attention人为的设定一小个范围。

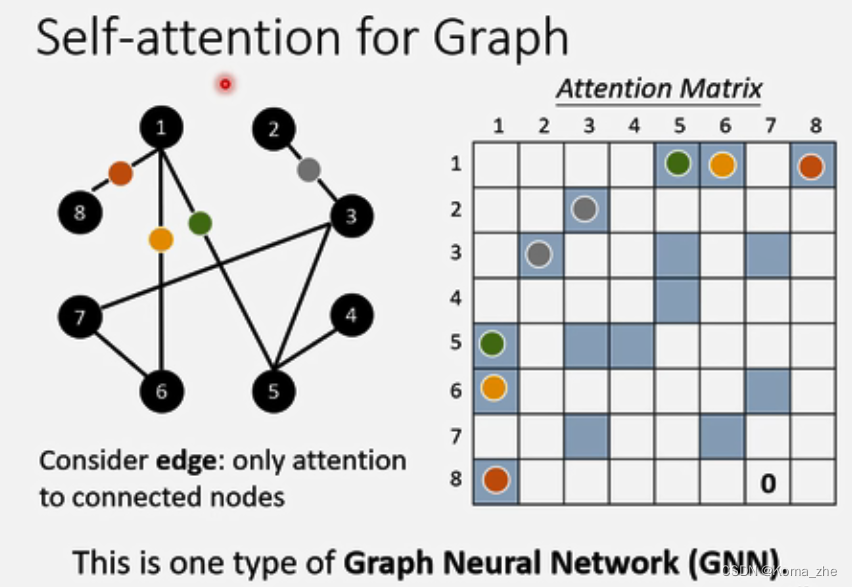
self-attention用于Graph上，结点和边对应到矩阵上，没有边对应的位置可以不计算attention score 直接设为0，这就是一种GNN