目录

• Gram矩阵简介
• 协方差矩阵
• Gram矩阵 和 协方差矩阵的关系
• Gram Matrix代码

Gram矩阵简介

gram矩阵是计算每个通道 i 的feature map与每个通道 j 的feature map 的内积
gram matrix的每个值可以说是代表 i 通道的feature map和 j 通道的 feature map的互相关程度。
参考博客

G=ATA=[a1Ta2T⋮anT][a1a2⋯an]=[a1Ta1a1Ta2⋯a1Tana2Ta1a2Ta2⋯a2TananTa1anTa2⋯anTan]G=A^{T} A=\left[\begin{array}{c} \mathbf{a}_{1}^{T} \\ \mathbf{a}_{2}^{T} \\ \vdots \\ \mathbf{a}_{n}^{T} \end{array}\right]\left[\begin{array}{llll} \mathbf{a}_{1} & \mathbf{a}_{2} & \cdots & \mathbf{a}_{n} \end{array}\right]=\left[\begin{array}{cccc} \mathbf{a}_{1}^{T} \mathbf{a}_{1} & \mathbf{a}_{1}^{T} \mathbf{a}_{2} & \cdots & \mathbf{a}_{1}^{T} \mathbf{a}_{n} \\ \mathbf{a}_{2}^{T} \mathbf{a}_{1} & \mathbf{a}_{2}^{T} \mathbf{a}_{2} & \cdots & \mathbf{a}_{2}^{T} \mathbf{a}_{n} \\ & & & \\ \mathbf{a}_{n}^{T} \mathbf{a}_{1} & \mathbf{a}_{n}^{T} \mathbf{a}_{2} & \cdots & \mathbf{a}_{n}^{T} \mathbf{a}_{n} \end{array}\right]G=ATA=⎣⎢⎢⎢⎡​a1T​a2T​⋮anT​​⎦⎥⎥⎥⎤​[a1​​a2​​⋯​an​​]=⎣⎢⎢⎡​a1T​a1​a2T​a1​anT​a1​​a1T​a2​a2T​a2​anT​a2​​⋯⋯⋯​a1T​an​a2T​an​anT​an​​⎦⎥⎥⎤​
上面的ai\mathbf{a}_{i}ai​均为列向量，i=1,2...ni=1,2...ni=1,2...n

对于上面的矩阵，就是一个矩阵自己的转置乘以自己。

协方差矩阵

建议先看懂这一篇：一文读懂 协方差矩阵
而协方差矩阵的求解步骤是：
1.对于Xn×dX_{n\times d}Xn×d​ ,先求每一列的均值
2.然后对应列减去此列的均值，得矩阵Cn×dC_{n\times d}Cn×d​
3.COVd×d=1n−1Cn×dTCn×d=1n−1(CT)d×nCn×dCOV_{d\times d}=\frac{1}{n-1}C_{n\times d}^{T}C_{n\times d}=\frac{1}{n-1}(C^{T})_{d\times n}C_{n\times d}COVd×d​=n−11​Cn×dT​Cn×d​=n−11​(CT)d×n​Cn×d​
也就是说协方差矩阵是先求均值，然后减去均值(作了一个中心化处理，白化)，再求协方差矩阵(除以1n−1\frac{1}{n-1}n−11​,即进行了标准化)

Gram矩阵 和 协方差矩阵的关系

• Gram矩阵和协方差矩阵的差别在于，Gram矩阵没有进行白化，也就是没有减去均值，而直接使用两个向量做内积。
• Gram矩阵和相关系数矩阵的差别在于，Gram矩阵既没有白化，也没有标准化(也就是除以两个向量的标准差)
• Gram Matrix实际上可以看做feature之间的偏心协方差矩阵(即没有减去均值的协方差矩阵)，在feature map中，每一个数字都来自于一个特定滤波器在特定位置的卷积，因此每个数字就代表一个特征的强度，而Gram计算的实际上是两两特征之间的相关性，哪两个特征是同时出现的，哪两个是此消彼长的等等，同时，Gram的对角线元素，还体现了每个特征在图像中出现的量，因此，Gram有助于把握整个图像的大体风格。有了表示风格的Gram Matrix，要度量两个图像风格的差异，只需比较他们Gram Matrix的差异即可。

这样，Gram所表达的意义和协方差矩阵相差不大，只是没有白化，标准化处理，显得比较粗糙。两个向量的协方差表示两个向量之间的相似程度，协方差越大越相似。对角线的元素值越大，表示其所代表的向量或者说特征越重要。

参考博客

参考博客

Gram Matrix详细解读

Gram Matrix代码

# Gram matrix格拉姆矩阵，是矩阵的内积运算，
# 在运算过后输入到此矩阵的特征图中的大的数字会变得更大，
# 这就相当于图片中的风格被放大了，放大的风格再参与损失计算，
# 能够对最后的合成图片产生更大的影响class Gram_matrix(nn.Module):def forward(self, input):batch, channel, height, weight = input.size()M = input.view(batch * channel, height * weight)gram = torch.mm(M, M.t())return gram.div(batch * channel * height * weight)# 代码来源： 深度学习之PyTorch实战计算机视觉  Chapter8

代码过程解释如下:

如上图所示：每个batch有3张图片，每张图片经过cnn后得到feature map的channel=6，把每个channel的图片给展平成一个向量，则一共有batch*channel个向量，即得到矩阵Mb∗c,h∗wM_{b*c, h*w}Mb∗c,h∗w​,矩阵M中的每一行就表示一个特征图展成的特征向量，每一列就代表一个feature map的总的像素个数.

torch.mm(M, M.t())的过程如下：

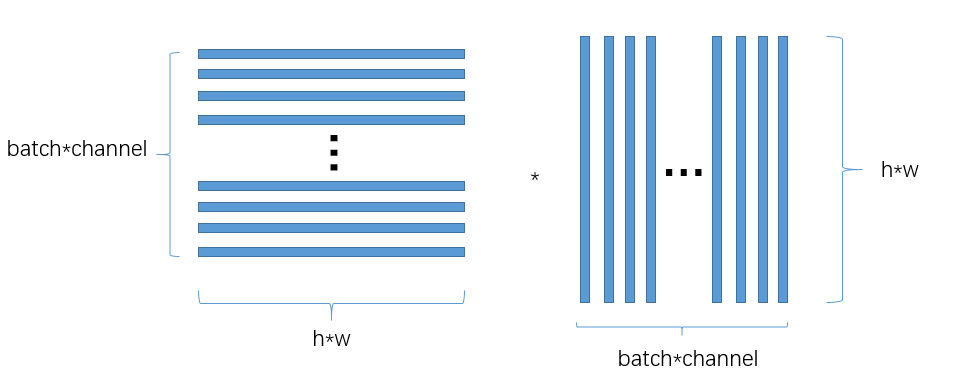
上面的是M∗MTM*M^{T}M∗MT，而协方差矩阵中是1n−1(CT)d×nCn×d\frac{1}{n-1}(C^{T})_{d\times n}C_{n\times d}n−11​(CT)d×n​Cn×d​,其实是一样的:因为M的每一行表示的是feature,即有b*c个feature variable. 而(CT)d×n(C^{T})_{d\times n}(CT)d×n​的每一行也表示feature,即(CT)d×n(C^{T})_{d\times n}(CT)d×n​有d个feature variable

也就是说：其实这里的M是对应着一文读懂协方差矩阵中的方法2。

看到这里,再去理解:

Gram Matrix实际上可以看做是feature之间的偏心协方差矩阵(即没有减去均值的协方差矩阵)， 在feature map中，每一个数字都来自于一个特定卷积核在特定位置的卷积，因此feature map 中的每个数字就代表此特征(一个channel的feature map展平后就叫一个特征)在此位置的强度，而Gram计算的实际上是两两fature之间的相关性，哪两个feature是同时出现的，哪两个是此消彼长的。同时，Gram Matrix的对角线元素体现了每个特征在图像中出现的量, 对角线的元素的值越大，表示其所代表的向量或者说特征越重要。因此Gram矩阵有助于把握整个图像的大体风格。
有了表示风格的Gram Matrix， 要度量两个图像风格的差异，只需比较他们的Gram Matrix的差异即可。

Gram Matrix的对角线元素提供了不同特征图（a1，a2 … ，an）各自的信息，其余元素提供了不同特征图之间的相关信息。

于是，在一个Gram矩阵中，既能体现出有哪些特征，又能体现出不同特征间的紧密程度。论文中作者把这个定义为风格。

Gram矩阵被用于表征图像的风格。在图像修复问题中，很常用的一项损失叫做风格损失（style loss），风格损失正是基于预测结果和真值之间的Gram矩阵的差异构建的。
参考博客