代码随想录刷题|买卖股票问题的总结
目录
总结
121.买卖股票的最佳时机
问题描述
特点分析
动态规划思路
122.买卖股票的最佳时机Ⅱ
问题描述
特点分析
动态规划思路
123.买卖股票的最佳时机III
问题描述
特点分析
动态规划思路
188.买卖股票的最佳时机IV
问题描述
特点分析
动态规划思路
309.最佳买卖股票时机含冷冻期
问题描述
特点分析
动态规划思路
714.买卖股票的最佳时机含手续费
问题描述
特点分析
动态规划思路
总结
0、题目描述
- 121. 买卖股票的最佳时机 只买卖一次
-
122. 买卖股票的最佳时机 II 可以买卖多次
-
123. 买卖股票的最佳时机 III 最多买卖 2 次
-
188. 买卖股票的最佳时机 IV 最多买卖 k 次
-
309. 最佳买卖股票时机含冷冻期 可以买卖多次,含冷冻期
-
714. 买卖股票的最佳时机含手续费 可以多次买卖,含手续费
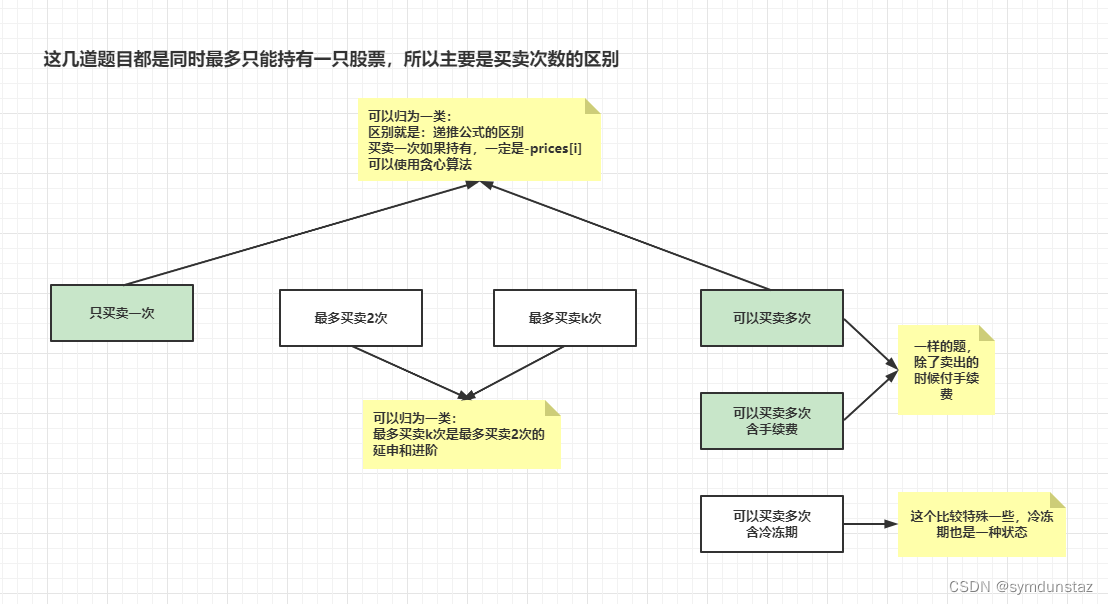
1、dp数组的含义
- dp数组的含义基本上都是,在第 i 天,状态 j下,手中现金的最大值为dp[i][j]
- 所以针对买卖股票问题,先画一个类似以下这样的表格,分清有几种状态
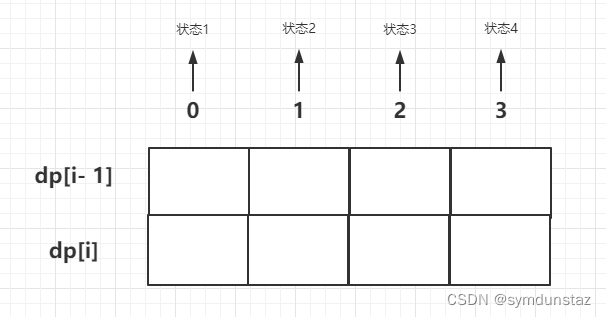
2、递推公式
- 递推公式基本上都是从前一天推后一天的内容
- 从这点来看的话,其中就指定最多买卖 k 次那道题目比较复杂,是对最多买卖两次的延申
- 先分析有几种状态,再分析达到第 i 天的每种状态有哪些情况,根据情况写出递推公式
3、初始化
- 初始化在 第 0 天 下,各个状态下手中现金的最大值
- 其实在第 0 天,主要分成两种情况就可以
- 要么是持有,那就-prices[0]
- 要么就是未持有,那就是0
- 如果是没有操作,也是 0
4、遍历方式
- 因为买卖股票的问题,都是从通过前一天的情况推导当天的情况,所以都是从前向后遍历
5、获取结果
- 未持有股票状态下比持有股票状态下的金钱多
- 买卖次数多比买卖次数少的金钱多
- 其中含冷冻期这道题目比较特殊,要对三种未持有股票状态进行比较
121.买卖股票的最佳时机
题目链接:力扣
问题描述
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
特点分析
- 只能买卖一次
- 可以暴力解法,超时
- 可以贪心算法,最右侧最大值 - 最左侧最小值
- 可以动态规划,
动态规划思路
dp[i][j] 表示在第 i 天,如果是状态 j , 手中的现金最大值为 dp[i][j],默认一开始手中的现金为0
状态分析
第 i 天有两种状态:持有股票、未持有股票
- 第 i 天持有股票
成为这种状态,要么前一天已经持有股票,要么今天才持有股票(新买的),选取其中的最大值- 情况一:前一天已经持有股票,dp[i][0] = dp[i - 1][0]
- 情况二:前一天未持有股票,要让今天持有股票,那就今天买,dp[i][0] = -prices[i]
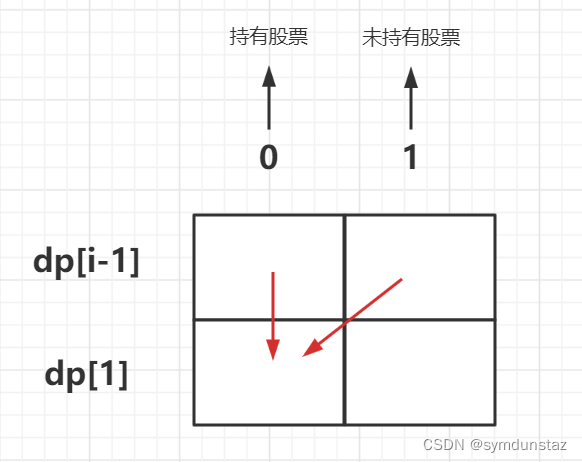
- 第 i 天未持有股票
成为这种状态,要么是前一天已经是未持有股票状态,要么今天才未持有状态(刚卖的),选取其中的最大值- 情况一:前一天已经是未持有状态,dp[i][1] = dp[i - 1][1]
- 情况二:前一天还是持有状态,要让今天是未持有状态,那就今天卖,那前一天肯定是持有状态,dp[i][1] = dp[i][0] + prices[i]
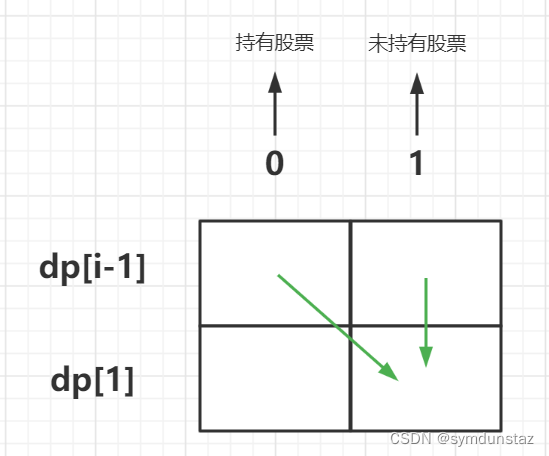
初始化
- 通过上面的状态分析,就可以获得dp数组的含义、递推公式
- 因为都是通过前一天获得的,所以就应该初始化第0天的状态
- 如果第 0 天持有股票,那肯定是买了,肯定花钱了,那就是 0 - prices[0]。因为手中一开始的钱就只有 0
- 如果第 0 天持有股票,那还没有花钱,那就是 0
获取结果
- 结果就是表中最后一天未持有股票时手中的最大现金数
- 因为不持有股票状态所得金钱一定比持有股票状态得到的多!
122.买卖股票的最佳时机Ⅱ
题目链接:力扣
问题描述
给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。
在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买,然后在 同一天 出售。
返回 你能获得的 最大 利润 。
特点分析
-
只能持有一只股票,可以买卖多次
-
可以贪心算法,只要能获利进行买卖
-
可以动态规划
动态规划思路
dp[i][j] 表示在第 i 天,如果是状态 j , 手中的现金最大值为 dp[i][j],默认一开始手中的现金为0
这道题目,第 i 天有两种状态:持有股票、未持有股票,和 121. 买卖股票的最佳时机 是一样的,不一样的是递推公式
先看,只可以买卖一次的递推公式
只买卖一次,有两种状态
第 i 天持有股票
情况一:前一天已经持有股票,dp[i][0] = dp[i - 1][0]
情况二:前一天未持有股票股票,dp[i][0] = -prices[i]
第 i 天未持有股票
情况一:前一天已经是未持有状态,dp[i][1] = dp[i - 1][1]
情况二:前一天还是持有股票状态,dp[i][1] = dp[i][0] + prices[i]
再看,可以买卖多次的递推公式
可以买卖多次,有两种状态
第 i 天持有股票
情况一:前一天已经持有股票,dp[i][0] = dp[i - 1][0]
情况二:前一天未持有股票股票,dp[i][0] = dp[i - 1][1] - prices[i]
第 i 天未持有股票
情况一:前一天已经是未持有状态,dp[i][1] = dp[i - 1][1]
情况二:前一天还是持有股票状态,dp[i][1] = dp[i][0] + prices[i]
这里和121. 买卖股票的最佳时机唯一不同的地方,就是推导dp[i][0]的时候,第i天买入股票的情况。
因为买卖股票的时候,可能已经出现前面获得利润的情况,不能从 0 开始买股票了,而是用前一天未持有股票的时候有的钱来买,这样才能将将前面的结果也进行累加
123.买卖股票的最佳时机III
题目链接:力扣
问题描述
给定一个数组,它的第 i 个元素是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
特点分析
- 最多可以完成两笔交易
- 可以动态规划
动态规划思路
dp[i][j] 表示在第 i 天,如果是状态 j , 手中的现金最大值为 dp[i][j],默认一开始手中的现金为0
状态分析
第 i 天有五种状态:但是也是主要分为持有股票和未持有股票,还有一个状态是没有操作
其中没有操作状态其实只用了一次,可以忽略,但是从下标 1 开始分析,更加方便,这样做最多 k 次买卖的时候也更加方便
- 没有操作
- 第一次买入(持有)
- 第一次卖出(未持有)
- 第二次买入(持有)
- 第二次卖出(未持有)
- 第 i 天是第一次买入
成为这种状态,要么第 i 天之前就已经第一次买入过了,要么第i 天新买的,选取其中的最大值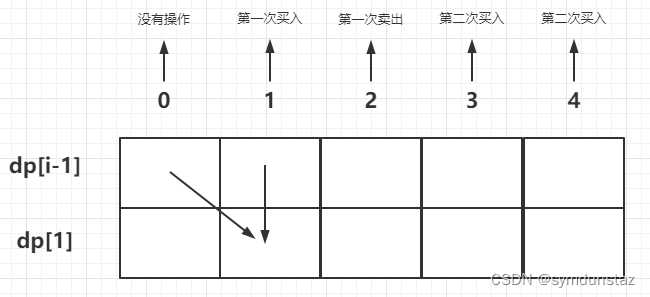
- 情况一:前面已经买好了,dp[i][0] = dp[i - 1][0]
- 情况二:第一次新买的,第i天买入股票了,那么dp[i][0] = - prices[i]
- 第 i 天是第一次卖出
成为这种状态,要么第 i 天之前已经第一次卖出过了,要么第 i 天新买的- 情况一:前面已经卖过了,dp[i][1] = dp[i - 1][1]
- 情况二:今天刚刚卖出,这种状态只能由第一次买入状态得到,那么dp[i][1] = dp[i - 1][0] + prices[i],
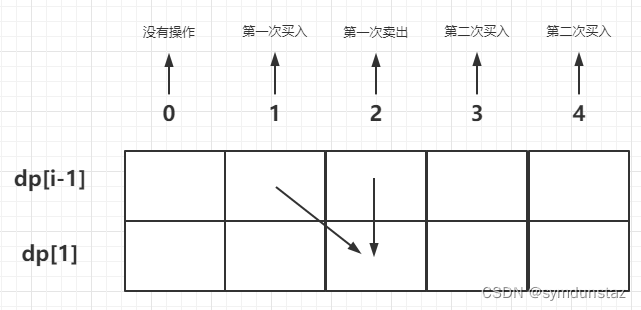
- 第 i 天是第二次买入
成为这种状态,要么第 i 天之前已经第二次买入过了,要么第 i 天就是第二次买入- 情况一:前面已经买好了,dp[i][2] = dp[i - 1][2]
- 情况二:今天刚买,那前天有肯定是第一次卖出的状态,那么dp[i][2] = dp[i - 1][1] - prices[i]
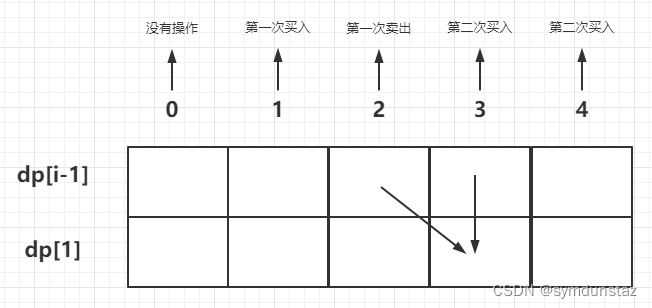
- 第 i 天是第二次卖出
成为这种状态,要么第 i 天之前已经第二次卖出过了,要么第 i 天就是第二次卖出- 情况一:前面已经第二次卖过了,dp[i][3] = dp[i - 1][3]
- 情况二:今天刚刚卖出,这种状态只能由第一次买入状态得到,那么dp[i][2] = dp[i - 1][2] + prices[i]
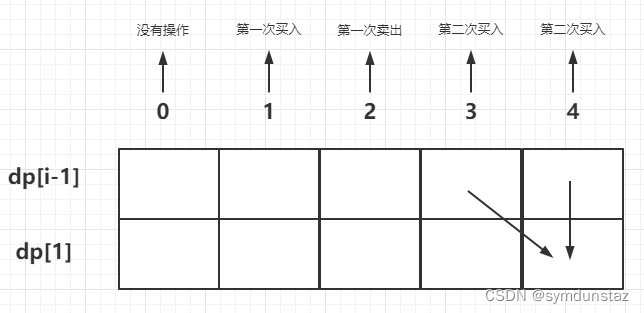
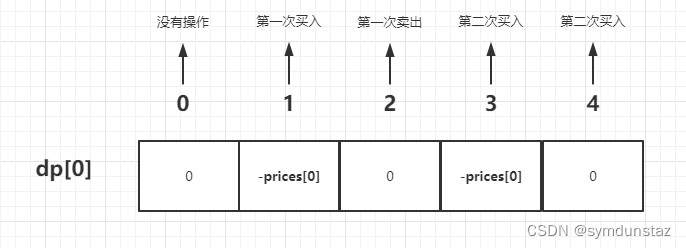
初始化
- 通过上面的状态分析,就可以获得dp数组的含义、递推公式
- 因为都是通过前一天获得的,所以就应该初始化第0天的状态
- 如果第 0 天持有股票,那肯定是买了,肯定花钱了,那就是 0 - prices[0]。因为手中一开始的钱就只有 0
- 如果第 0 天持有股票,那还没有花钱,那就是 0
获取结果
- 结果就是表中最后一天 第二次卖出状态下 手中的最大现金数
- 因为不持有股票状态所得金钱一定比持有股票状态得到的多!
- 第二次卖出肯定比其他状态下的金钱多
188.买卖股票的最佳时机IV
题目链接:力扣
问题描述
给定一个整数数组 prices ,它的第 i 个元素 prices[i] 是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
特点分析
- 最多可以完成 k 笔交易
- 可以动态规划
动态规划思路
状态分析
- 其实这道题目和 123. 买卖股票的最佳时机 III 是原理一样的,只不过是维度上的拓宽
- 状态也是分为 没有操作、持有状态 、未持有股票状态
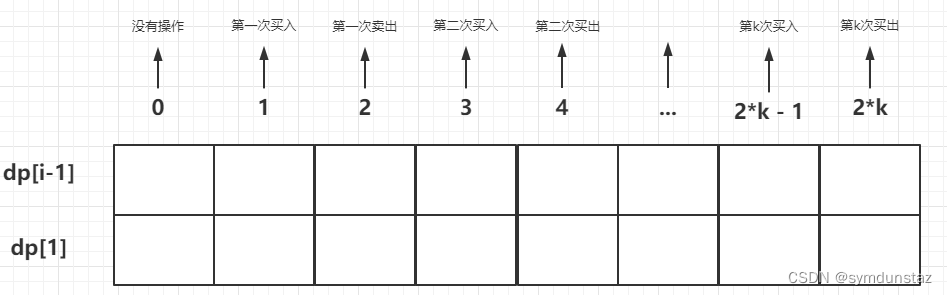
- 从下标 1 开始两两为一组买入、卖出状态
- 找到上一道题目的规律就可以
-
for (int j = 0; j < 2 * k - 1; j += 2) {dp[i][j + 1] = max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);dp[i][j + 2] = max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]); }
-
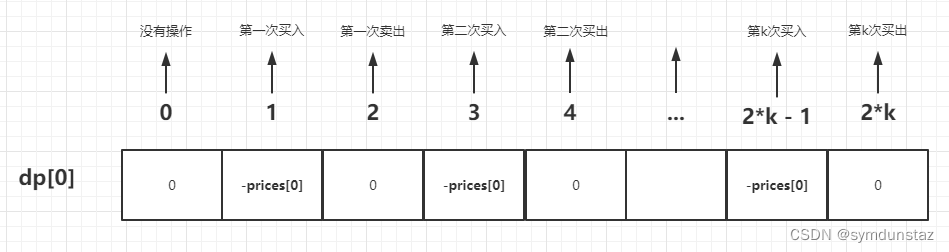
初始化
- 通过上面的状态分析,就可以获得dp数组的含义、递推公式
- 因为都是通过前一天获得的,所以就应该初始化第0天的状态
- 如果第 0 天持有股票,那肯定是买了,肯定花钱了,那就是 0 - prices[0]。因为手中一开始的钱就只有 0
- 如果第 0 天持有股票,那还没有花钱,那就是 0
获取结果
- 结果就是表中最后一天 第k次卖出状态下 手中的最大现金数
- 因为不持有股票状态所得金钱一定比持有股票状态得到的多!
- 第k次卖出肯定比其他状态下的金钱多
309.最佳买卖股票时机含冷冻期
题目链接:力扣
问题描述
给定一个整数数组prices,其中第 prices[i] 表示第 i 天的股票价格 。
设计一个算法计算出最大利润。在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票):
卖出股票后,你无法在第二天买入股票 (即冷冻期为 1 天)。
特点分析
- 可以多次买卖,卖出后冷冻期为1天
- 可以动态规划
动态规划思路
dp[i][j] 表示在第 i 天,如果是状态 j , 手中的现金最大值为 dp[i][j],默认一开始手中的现金为0
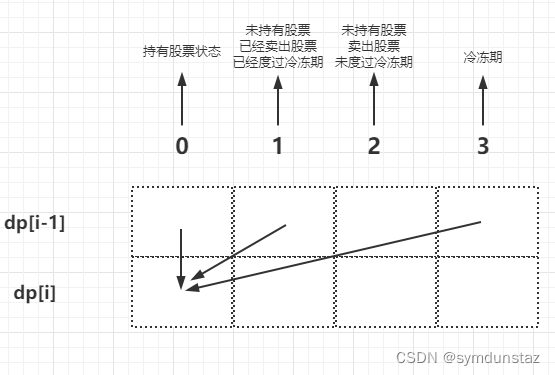
状态分析
第 i 天有五种状态:可以分为 持有股票状态 和 未持有股票状态
- 持有股票状态(持有)
- 未持有股票状态,并且过了冷冻期(未持有)
- 未持有股票状态,还没过冷冻期,表示今天刚卖出(未持有)
- 冷冻期状态(未持有)
- 第 i 天是持有股票状态
成为这种状态,要么之前已经买过了,要么今天买(今天可以买,要么前一天是冷冻期,要么前一天还是未持有股票状态并且多了冷冻期),选取其中最大的- 情况一:之前已经买入了股票,dp[i][0] = dp[i - 1][0]
- 情况二:今天买
- 前一天是冷冻期:dp[i][0] = dp[i - 1][3] - prices[i]
- 前一天是未持有状态:dp[i][0] dp[i - 1][1] -prices[i]
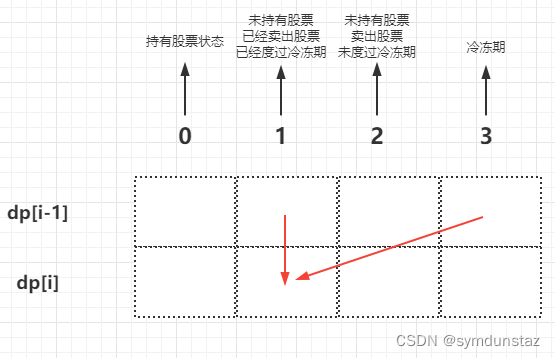
- 第 i 天是未持有股票状态,并且过了冷冻期
成为这种状态,要么前一天就是状态二(未持有股票状态,并且过了冷冻期),要么前一天是冷冻期(状态四),今天就成为了状态二- 情况一:前一天已经是状态二,dp[i][1] = dp[i - 1][1]
- 情况二:前一天是冷冻期,dp[i][1] = dp[i - 1][3]
- 第 i 天是未持有股票状态,还没过冷冻期
成为这种状态,是今天刚卖出股票,所以前一天是持有股票状态的,只能从状态一获取到- 情况:前一天是持有股票状态,dp[i][2] = dp[i - 1][0] + prices[i]
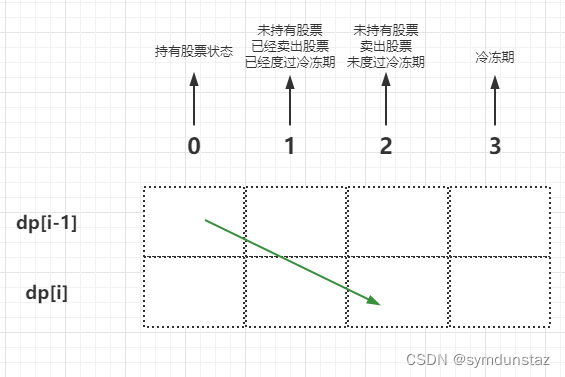
- 情况:前一天是持有股票状态,dp[i][2] = dp[i - 1][0] + prices[i]
- 第 i 天是冷冻期
成为这种状态,就是前一天刚卖出股票,只能从状态三获得到- 情况:前一天卖股票,dp[i][3] = dp[i - 1][2]
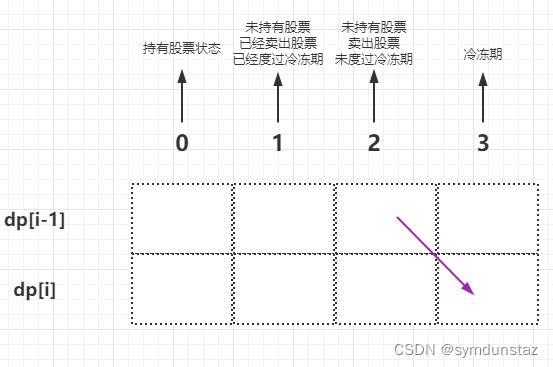
- 情况:前一天卖股票,dp[i][3] = dp[i - 1][2]
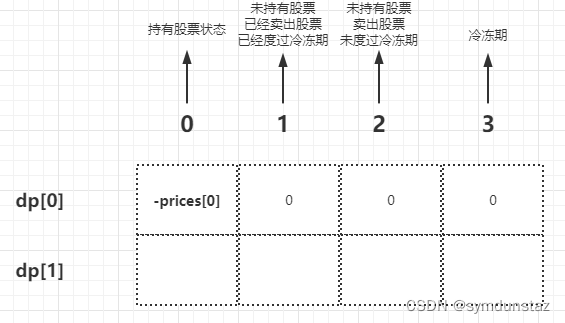
初始化
- 通过上面的状态分析,就可以获得dp数组的含义、递推公式
- 因为都是通过前一天获得的,所以就应该初始化第0天的状态
- 如果第 0 天持有股票,那肯定是买了,肯定花钱了,那就是 0 - prices[0]。因为手中一开始的钱就只有 0
- 如果第 0 天持有股票,那还没有花钱,那就是 0
获取结果
- 因为不持有股票状态所得金钱一定比持有股票状态得到的多!
- 但是这几个未持有股票的状态无法像之前的题目分出那个最大,只能通过程序获取
714.买卖股票的最佳时机含手续费
题目链接:力扣
问题描述
给定一个整数数组 prices,其中 prices[i]表示第 i 天的股票价格 ;整数 fee 代表了交易股票的手续费用。
你可以无限次地完成交易,但是你每笔交易都需要付手续费。如果你已经购买了一个股票,在卖出它之前你就不能再继续购买股票了。
返回获得利润的最大值。
注意:这里的一笔交易指买入持有并卖出股票的整个过程,每笔交易你只需要为支付一次手续费。
特点分析
- 可以买卖多次,每笔交易需要手续费
- 可以贪心算法
- 可以动态规划
动态规划思路
与122. 买卖股票的最佳时机 II 原理一样,只需要再卖出时付手续费就可以