从四个子空间角度理解SVD

A=Um×mΣm×nVn×nTA =U_{m \times m}\Sigma_{m \times n}V_{n \times n}^TA=Um×m​Σm×n​Vn×nT​

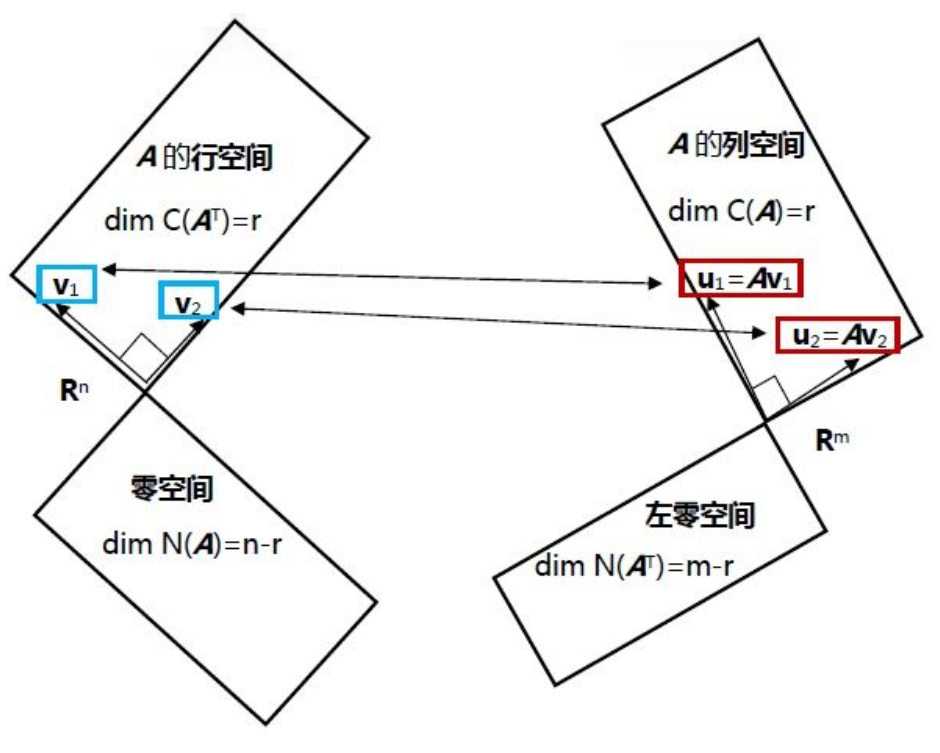
将A\mathbf {A}A视为线性变换，并将整个Rn\mathbf R^nRn空间拆分为两部分，即A\mathbf {A}A的行空间（维数rrr）和零空间（维数n−rn-rn−r，行空间的正交补）：

1. A\mathbf {A}A的行空间中，存在第一部分标准正交基vi(i=1,2,...,r)\mathbf{v}_{i}(i=1,2,...,r)vi​(i=1,2,...,r)
   A\mathbf AA对应的线性变换将行空间中的vi\mathbf{v}_{i}vi​映射为A\mathbf AA的列空间中的一个非零向量σiui=Avi\sigma_i\mathbf u_i=\mathbf A\mathbf{v}_{i}σi​ui​=Avi​（视为对A\mathbf AA的列向量的线性组合）；
   A[v1v2⋯vr]=[σ1u1σ2u2⋯σrur]=[u1u2⋯ur][σ1σ2⋱σr]\begin{aligned}\boldsymbol{A}\left[\begin{array}{llll}\mathbf{v}_{1} & \mathbf{v}_{2} & \cdots & \mathbf{v}_{r}\end{array}\right] &=\left[\begin{array}{lllll} \sigma_{1} \mathbf{u}_{1} & \sigma_{2} \mathbf{u}_{2} & \cdots & \sigma_{r} \mathbf{u}_{r} \end{array}\right] \\ &=\left[\begin{array}{lllll} \mathbf{u}_{1} & \mathbf{u}_{2} & \cdots & \mathbf{u}_{r} \end{array}\right]\left[\begin{array}{llll} \sigma_{1} & & & \\ & \sigma_{2} & & \\ & & \ddots & \\ & & & \sigma_{r} \end{array}\right] \end{aligned}A[v1​​v2​​⋯​vr​​]​=[σ1​u1​​σ2​u2​​⋯​σr​ur​​]=[u1​​u2​​⋯​ur​​]⎣⎢⎢⎡​σ1​​σ2​​⋱​σr​​⎦⎥⎥⎤​​
   此即Um×nV^n×r=U^m×rΣ^r×r\mathbf U_{m\times n}\hat{\mathbf V}_{n\times r}=\hat{\mathbf U}_{m\times r}\hat{\mathbf \Sigma}_{r\times r}Um×n​V^n×r​=U^m×r​Σ^r×r​，对应下图中的红色部分

注意，A\mathbf AA的行空间中的向量x\mathbf xx到列空间中的向量Ax\mathbf A\mathbf xAx映射，为一一映射
也就是说对于行空间中的向量x≠y\mathbf x\neq\mathbf yx​=y，则必有列空间中的向量Ax≠Ay\mathbf A\mathbf x\neq\mathbf A\mathbf yAx​=Ay
证明：
反证法：对于行空间的向量x≠y\mathbf x\neq\mathbf yx​=y，假设有Ax=Ay\mathbf A\mathbf x=\mathbf A\mathbf yAx=Ay
则A(x−y)=0\mathbf A(\mathbf x-\mathbf y)=\mathbf 0A(x−y)=0，这就是说，向量(x−y)(\mathbf x-\mathbf y)(x−y)在零空间中；
另一方面，向量(x−y)(\mathbf x-\mathbf y)(x−y)一定在行空间中（两个行空间中的向量的线性组合）
向量(x−y)(\mathbf x-\mathbf y)(x−y)不可能既在行空间中，又在零空间中，因此假设不成立

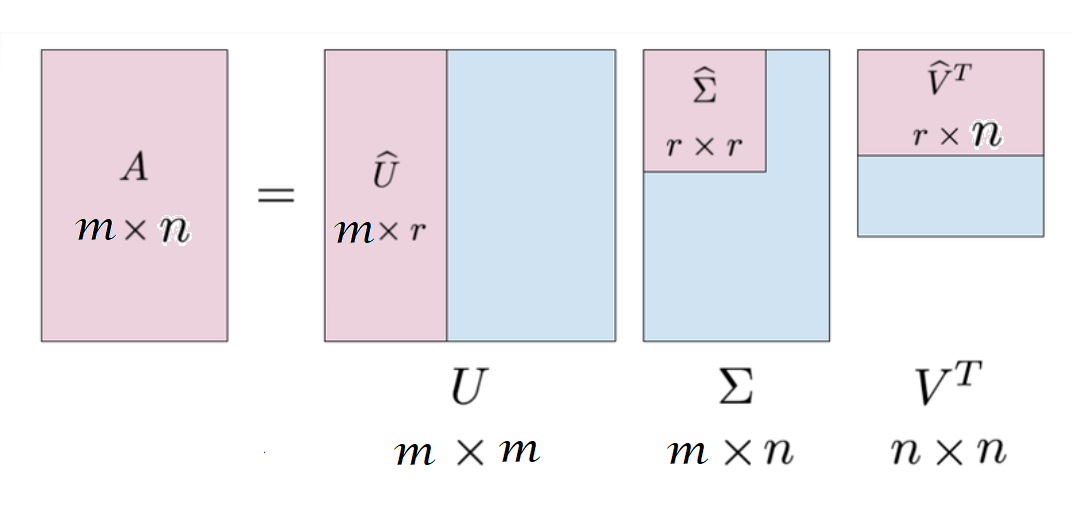
2. A\mathbf AA的零空间中，有第二部分标准正交基vi(i=r+1,r+2,...,n)\mathbf v_i(i=r+1,r+2,...,n)vi​(i=r+1,r+2,...,n)
A\mathbf AA对应的线性变换将vi\mathbf v_ivi​映射为零向量，满足Avi=0\mathbf {A}\mathbf v_i=0Avi​=0；
体现在Σm×n\boldsymbol{\Sigma}_{m\times n}Σm×n​中，就是其右下角的0元素，对应上图蓝色部分

结论

我们在A\boldsymbol{A}A的四个子空间中，寻找了两组合适的基：

• 第一组标准正交基由两部分构成：
  vi(i=1,2,...,r)\mathbf{v}_{i}(i=1,2,...,r)vi​(i=1,2,...,r)为行空间中的标准正交基
  vi(i=r+1,r+2,...,n)\mathbf{v}_{i}(i=r+1,r+2,...,n)vi​(i=r+1,r+2,...,n)为零空间中的标准正交基
• 第二组标准正交基由两部分构成：
  ui(i=1,2,...,r)\mathbf{u}_{i}(i=1,2,...,r)ui​(i=1,2,...,r)为列空间中的标准正交基
  ui(i=r+1,r+2,...,m)\mathbf{u}_{i}(i=r+1,r+2,...,m)ui​(i=r+1,r+2,...,m)为左零空间中的标准正交基

理论的统一

前面笔记10-1说过，SVD（A=UΣVT\boldsymbol{A} =\boldsymbol{U} \boldsymbol{\Sigma} \boldsymbol{V}^{T}A=UΣVT）中，Σ\boldsymbol{\Sigma}Σ奇异值σ≥0\sigma\geq 0σ≥0；
并且，若A\boldsymbol{A}A为可逆矩阵r=nr=nr=n，则ATA\boldsymbol{A}^{T} \boldsymbol{A}ATA和AAT\boldsymbol{A}\boldsymbol{A}^{T}AAT为正定矩阵，其特征值全为正，对应A\boldsymbol{A}A奇异值全为正；
若A\boldsymbol{A}A为不可逆矩阵r

因此有：
A\boldsymbol{A}A不可逆（r Σ\boldsymbol{\Sigma}Σ对角元为正数和0（存在奇异值为0）⟺\iff⟺
A\boldsymbol{A}A存在零空间（维度n−r>0n-r>0n−r>0），零空间中的一部分向量vi\mathbf v_ivi​被线性变换A\boldsymbol{A}A映射为零向量（Avi=0\boldsymbol{A}\mathbf v_i=0Avi​=0）