一、题目描述

一只青蛙一次可以跳上1级台阶，也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。

答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。

二、示例

示例 1：

输入：n = 2
输出：2
示例 2：

输入：n = 7
输出：21
示例 3：

输入：n = 0
输出：1

0 <= n <= 100

三、题目分析 & 解题思路

根据题目描述 可做以下规律推导
当 为 n 阶台阶
n = 1
跳法 ：1 种 ( 1)
n = 2
跳法 : 2种 ( 1 + 1 或 2)
n = 3
跳法：3种 ( 1+ 1 + 1 或 1 + 2 或 2 +1)
n = 4
跳法：5 种( 1+1+1+1 或 1+2+1 或 2+1+1 或 1+1+2 或 2+2)
n = 5
跳法：8种 (1+1+1+1+1 或 1+2+1+1 或 1+1+2+1 或 1+1+1+2 或 2+1+1+1 或 2+2+1或2+1+2 或 1+2+2)

大家可以发现 随着 n 的逐渐加1 青蛙的跳法 也是 逐渐增加 且 增加得 具体跳法 有着以下这样得规律

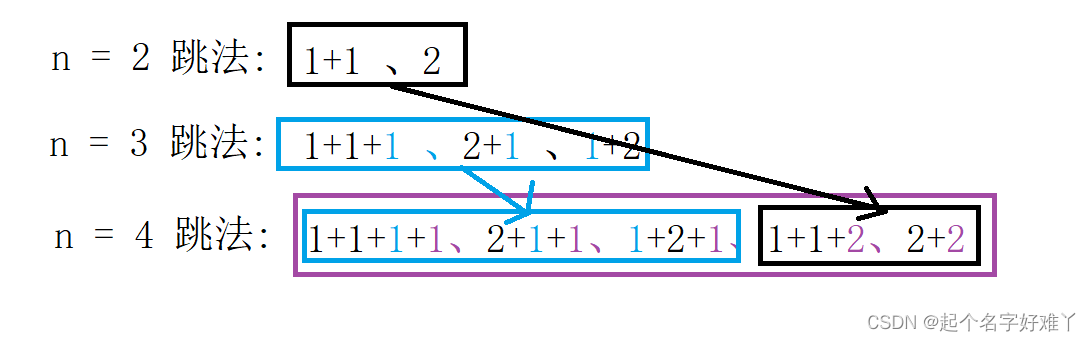
通过规律可以发现
n = 4 跳法 其实就是 n = 3 的每种跳法的基础上 加 1 再加上 n = 2 的每种跳法的基础上 加 2

由此 我们可以 推导出 公式

n 个台阶的跳法为 f(n) = f(n-2) + f(n-1)

看到这里其实不难发现 n 个台阶的 跳法 其实就是 斐波那契数列
同样可以使用递归的方法，也可以使用循环相加的方法计算出 n 个台阶的 跳法个数

代码实现

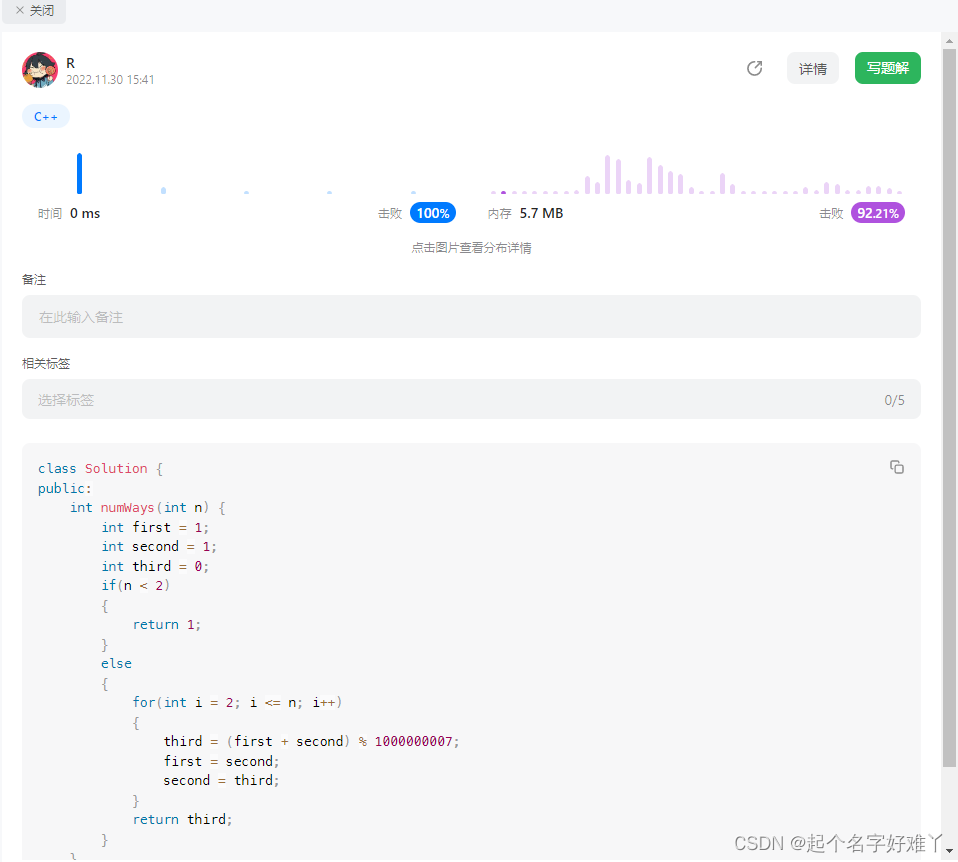
循环相加方法

class Solution {
public:int numWays(int n) {int first = 1;int second = 1;int third = 0;if(n < 2){return 1;}else{for(int i = 2; i <= n; i++){third = (first + second) % 1000000007;first = second;second = third;}return third;}}
};

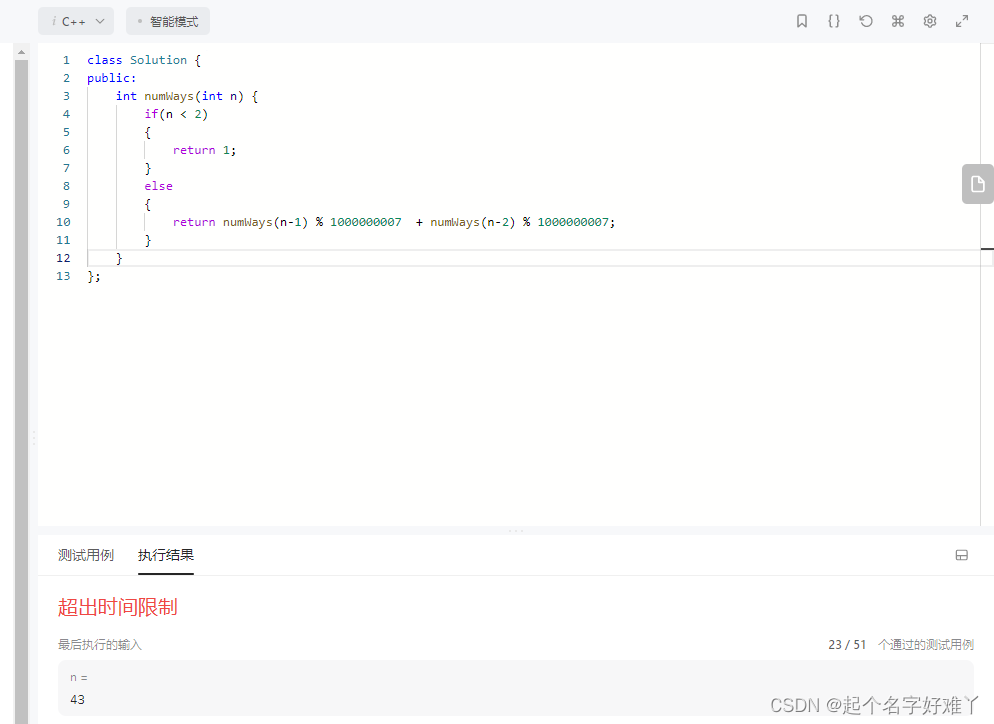
迭代

class Solution {
public:int numWays(int n) {if(n < 2){return 1;}else{return numWays(n-1) % 1000000007  + numWays(n-2) % 1000000007;}}
};

但是由于迭代的时间复杂度过高 会超出时间限制